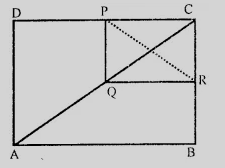
如圖所示,$ABCD$ 和 $PQRC$ 是矩形,$Q$ 是 $AC$ 的中點。
證明 $DP = PC$。
 "\n
"\n
已知
$ABCD$ 和 $PQRC$ 是矩形,$Q$ 是 $AC$ 的中點。
要求
我們必須證明 $DP = PC$。
解答
在 $\triangle ACD$ 中,
$Q$ 是 $AC$ 的中點,且 $QP \parallel AD$。
這意味著,
$P$ 是 $CD$ 的中點。
因此,
$DP = PC$
證畢。

廣告
 "\n
"\n已知
$ABCD$ 和 $PQRC$ 是矩形,$Q$ 是 $AC$ 的中點。
要求
我們必須證明 $DP = PC$。
解答
在 $\triangle ACD$ 中,
$Q$ 是 $AC$ 的中點,且 $QP \parallel AD$。
這意味著,
$P$ 是 $CD$ 的中點。
因此,
$DP = PC$
證畢。
