在下圖中，\( O \) 是圓弧的圓心，\( AOB \) 是一條直線。求陰影區域的周長和麵積，精確到小數點後一位。(取 \( \pi=3.142) \)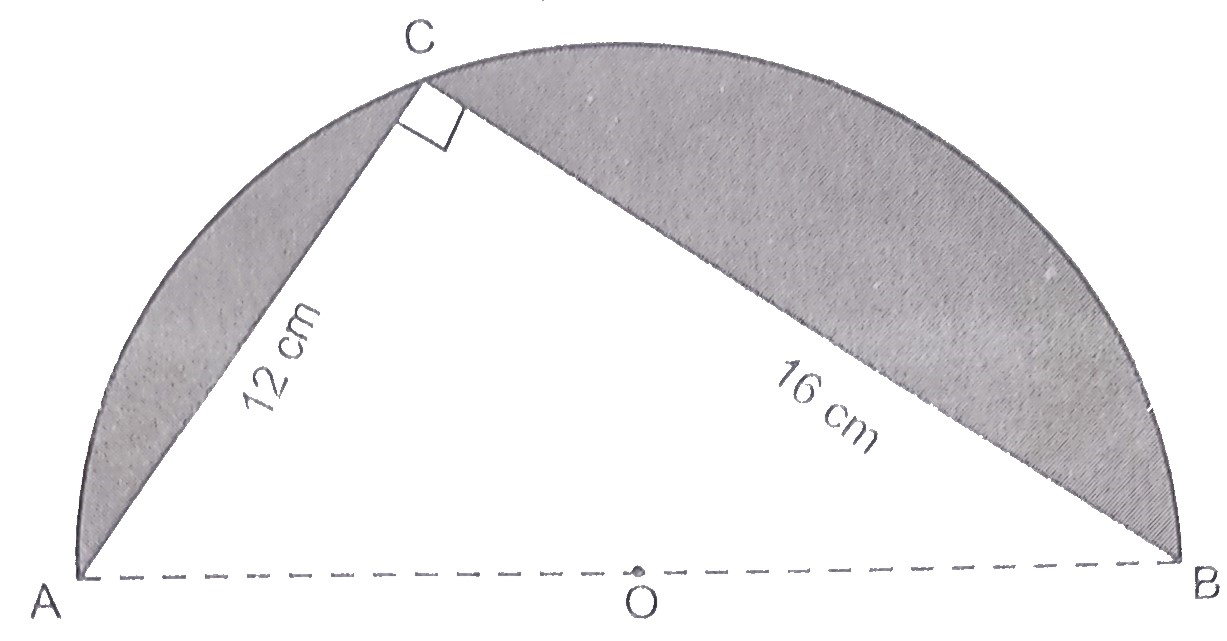

已知

\( O \) 是圓弧的圓心，\( AOB \) 是一條直線。

要求：

我們必須求出陰影區域的周長和麵積，精確到小數點後一位。

解答

在直徑AB上作一個半圓
在這個半圓內畫出三角形ACB。

在直角三角形ACB中，根據勾股定理，

$AB=\sqrt{\mathrm{AC}^{2}+\mathrm{BC}^{2}}$

$=\sqrt{(12)^{2}+(16)^{2}}$

$=\sqrt{144+256}$

$=\sqrt{400}$

$=20 \mathrm{~cm}$

因此，

半圓的半徑 $=\frac{20}{2}$

$=10 \mathrm{~cm}$

陰影區域的周長 = 半圓的周長 + AC + BC

$=\pi r+12+16$

$=3.142 \times 10+28$

$=31.42+28 \mathrm{~cm}$

$=59.42$

$=59.4 \mathrm{~cm}$

陰影區域的面積 = 半圓的面積 - 三角形ABC的面積

$=\frac{1}{2} \pi r^{2}-\frac{1}{2} \times 12 \times 16$

$=\frac{1}{2} \times 3.142 \times 10^2 - 96$

$=\frac{314.2}{2}-96$

$=157.1-96$

$=157.1 - 96 = 61.1 \mathrm{~cm}^{2}$

陰影區域的周長和麵積精確到小數點後一位分別為 59.4 cm 和 61.1 cm²。

更新於：2022年10月10日

瀏覽量：222

開啟你的職業生涯

完成課程獲得認證

開始學習
廣告