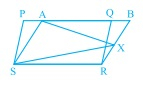
在下圖中，PQRS 和 ABRS 是平行四邊形，X 是 BR 邊上的任意一點。
(i) ar(PQRS) = ar(ABRS)
(ii) ar(AXS) = 1/2 ar(PQRS)

已知

PQRS 和 ABRS 是平行四邊形，X 是 BR 邊上的任意一點。

要求

我們必須證明：

(i) ar(PQRS) = ar(ABRS)
(ii) ar(AXS) = 1/2 ar(PQRS)

解答

(i) 平行四邊形 PQRS 和 ABRS 具有相同的底 SR，並且位於相同的平行線 SR 和 PB 之間。

這意味著：

ar(PQRS) = ar(ABRS)……(i)

(ii) 在平行四邊形 ABRS 中，

△AXS 和平行四邊形 ABRS 具有相同的底 AS，並且位於相同的平行線 AS 和 BR 之間。

這意味著：

ar(△AXS) = 1/2 ar(平行四邊形ABRS)……(ii)

由 (i) 和 (ii) 可得：

ar(△AXS) = 1/2 ar(平行四邊形 PQRS)

教程點

更新於：2022年10月10日

28 次瀏覽

開啟您的職業生涯

完成課程獲得認證

開始學習