資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究在下圖中，\( \mathrm{P} \) 是平行四邊形 \( \mathrm{ABCD} \) 內部的一點。
(i) \( \operatorname{ar}(\mathrm{APB})+\operatorname{ar}(\mathrm{PCD})=\frac{1}{2} \operatorname{ar}(\mathrm{ABCD}) \)
(ii) \( \operatorname{ar}(\mathrm{APD})+\operatorname{ar}(\mathrm{PBC})=\operatorname{ar}(\mathrm{APB})+\operatorname{ar}(\mathrm{PCD}) \)
[提示：過 \( \mathrm{P} \)，作一條平行於 \( \mathrm{AB} \) 的直線。]
"\n
已知
\( \mathrm{P} \) 是平行四邊形 \( \mathrm{ABCD} \) 內部的一點。
要求
我們需要證明
(i) \( \operatorname{ar}(\mathrm{APB})+\operatorname{ar}(\mathrm{PCD})=\frac{1}{2} \operatorname{ar}(\mathrm{ABCD}) \)
(ii) \( \operatorname{ar}(\mathrm{APD})+\operatorname{ar}(\mathrm{PBC})=\operatorname{ar}(\mathrm{APB})+\operatorname{ar}(\mathrm{PCD}) \)
解答
作兩條直線 $EF$ 和 $GH$，分別平行於 $AB$ 和 $BC$。
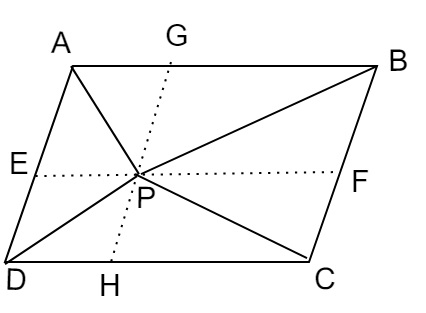
(i) $\triangle APB$ 和平行四邊形 $AEFB$ 共底 $AB$，且在同一對平行線 $AB$ 和 $EF$ 之間。
這意味著，
$ar (\triangle APB) = \frac{1}{2} ar (AEFB)$...….(i)
$\triangle DPC$ 和平行四邊形 $EFCD$ 共底 $DC$，且在同一對平行線 $DC$ 和 $EF$ 之間。
這意味著，
$ar (\triangle DPC) = \frac{1}{2} ar (EFCD)$...….(ii)
將 (i) 和 (ii) 相加，得到：
$ar (\triangle APB)+ ar (\triangle DPC) = \frac{1}{2} ar (AEFB)+\frac{1}{2} ar (EFCD)$
$ar (\triangle APB)+ ar (\triangle DPC) = \frac{1}{2}( ar (AEFB)+ar (EFCD)$
$ar (\triangle APB)+ ar (\triangle DPC) = \frac{1}{2} ar (ABCD)$..........(iii)
(ii) $\triangle APD$ 和平行四邊形 $AGHD$ 共底 $AD$，且在同一對平行線 $AD$ 和 $GH$ 之間。
這意味著，
$ar (\triangle APD) = \frac{1}{2} ar (AGHD)$...….(iv)
$\triangle PBC$ 和平行四邊形 $GBCH$ 共底 $BC$，且在同一對平行線 $BC$ 和 $GH$ 之間。
這意味著，
$ar (\triangle PBC) = \frac{1}{2} ar (GBCH)$...….(v)
將 (iv) 和 (v) 相加，得到：
$ar (\triangle APD)+ ar (\triangle PBC) = \frac{1}{2} ar (AGHD)+\frac{1}{2} ar (GBCH)$
$ar (\triangle APD)+ ar (\triangle PBC) = \frac{1}{2}[ ar (AGHD)+ar (GBCH)]$
$ar (\triangle APD)+ ar (\triangle PBC) = \frac{1}{2} ar (ABCD)$............(vi)
(iii) 從 (iii) 和 (vi) 中，我們得到：
$ar (\triangle APB)+ ar (\triangle DPC) =ar (\triangle APD)+ ar (\triangle PBC)$
41 次檢視
