資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學在下圖中，$AP \| BQ \| \mathrm{CR}$。證明\( \operatorname{ar}(\mathrm{AQC})=\operatorname{ar}(\mathrm{PBR}) \)。
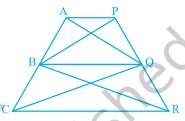
已知
$AP \| BQ \| \mathrm{CR}$。
要求
我們必須證明\( \operatorname{ar}(\mathrm{AQC})=\operatorname{ar}(\mathrm{PBR}) \)。
解答
$\triangle BQC$ 和 $\triangle BQR$ 位於同底 $BQ$ 上，且在平行線 $BQ$ 和 $CR$ 之間。
因此，
$ar(\triangle BQR) = ar(\triangle BQC)$.....…(i)
$\triangle AQB$ 和 $\triangle PBQ$ 位於同底 $BQ$ 上，且在平行線 $BQ$ 和 $AP$ 之間。
因此，
$ar(\triangle ABQ) = ar(\triangle PBQ)$.....…(ii)
從給定圖形中，我們得到，
$ar (\triangle PBR) = ar (\triangle PBQ) + ar (\triangle QBR)$......…..(iii)
$ar(\triangle AQC) = ar (\triangle AQB)+ ar (\triangle BQC)$.......…(iv)
將 (i) 和 (ii) 相加，我們得到，
$ar (\triangle BQC) + ar(\triangle AQB) = ar (\triangle QBR) + ar (\triangle PBQ)$
$ar(\triangle AQC) = ar(\triangle PBR)$ [根據 (iii) 和 (iv)]
證畢。
更新於：2022年10月10日
46 次瀏覽
廣告