資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究在三角形\( \mathrm{ABC} \)中，\( \mathrm{E} \)是中線AD的中點。證明\( \operatorname{ar}(\mathrm{BED})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC}) \)。
已知
在三角形\( \mathrm{ABC} \)中，\( \mathrm{E} \)是中線AD的中點。
要求
我們需要證明\( \operatorname{ar}(\mathrm{BED})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC}) \)。
解答
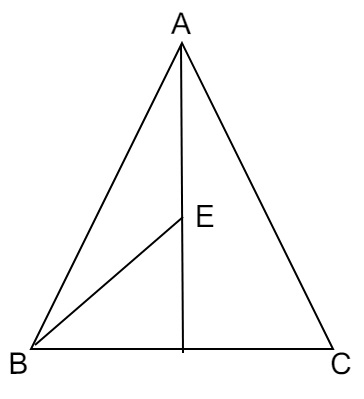
我們知道，
中線將三角形分成兩個面積相等的三角形。
這意味著，
$\operatorname{ar}(\triangle \mathrm{ABD})=\operatorname{ar}(\triangle \mathrm{ADC})=\frac{1}{2} \operatorname{ar}(\triangle \mathrm{ABC})$............(i)
在$\triangle \mathrm{ABD}$中
$\mathrm{BE}$是中線。
這意味著，
$\operatorname{ar}(\triangle \mathrm{BED})=\operatorname{ar}(\triangle \mathrm{BAE})=\frac{1}{2} \operatorname{ar}(\triangle \mathrm{ABD})$
$\Rightarrow \operatorname{ar}(\triangle \mathrm{BED})= \frac{1}{2}[\frac{1}{2}ar(\triangle \mathrm{ABC})]$ [由(i)得]
$\operatorname{ar}(\triangle \mathrm{BED})=\frac{1}{4} \operatorname{ar}(\triangle \mathrm{ABC})$
證畢。
更新於: 2022年10月10日
57 次瀏覽
廣告