資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學從一座垂直塔的頂部，同時觀察到與塔底在同一直線上的兩輛汽車的俯角分別為 $ 45^{o}$ 和 $ 60^{o}$。如果這兩輛車相距 100 米，並且都在塔的同一側，求塔的高度。$ \left( 使用\ \sqrt{3} =1.73\right)$
已知：一座垂直塔和從塔頂觀察到的兩輛車的俯角 $\angle ABC=45^{o}$ 和 $\angle ADC=60^{o}$，兩車之間的距離 $BD=100$ 米。
.
求解：求塔的高度。
解
設 AC 為塔的高度。B、D 為兩車所在的位置。
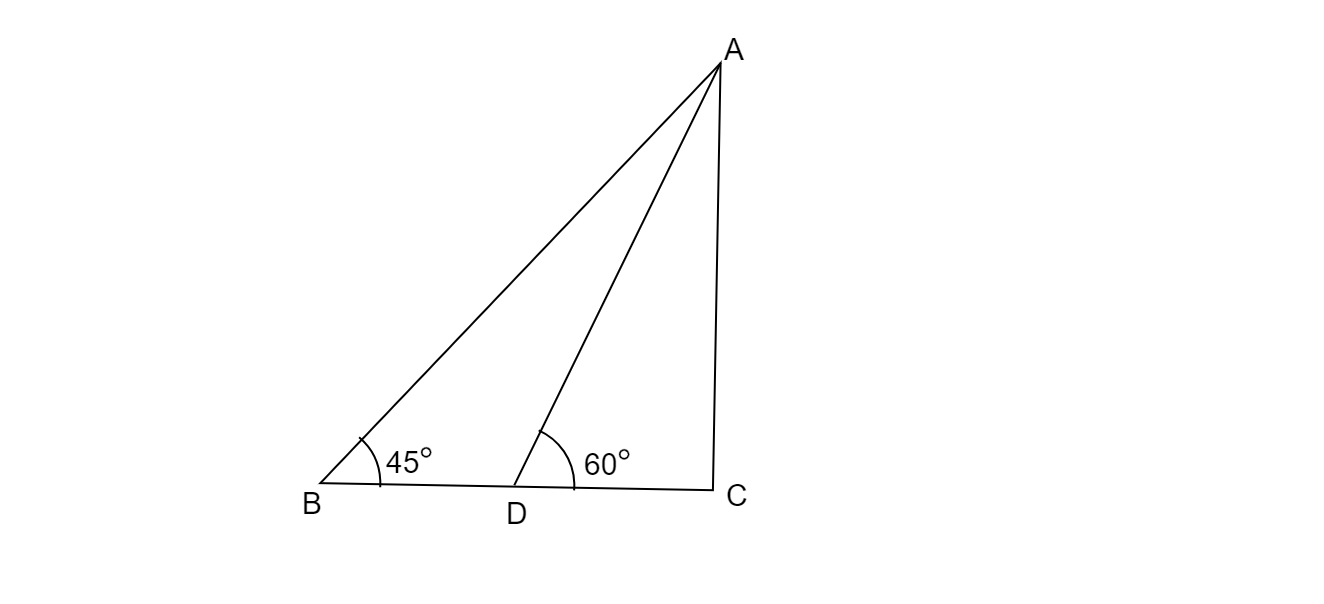
已知兩車之間的距離，$BD=100$ 米
$\angle ABC=45^{o} \ and\ \angle ADC=60^{o}$
在 $\vartriangle ADC$ 中，$tan60^{o} =\frac{AC}{DC} =\sqrt{3}$ $\left( \because \ tan60^{o} =\sqrt{3}\right)$
$\Rightarrow DC=\frac{AC}{\sqrt{3}}$
在 $\vartriangle ABC$ 中，$tan45^{o} =\frac{AC}{BC} =1$ $( \because \ tan45^{o} =1)$
$\Rightarrow AC=BC$
且 $BC=BD+DC$
$\Rightarrow AC=BD+\frac{AC}{\sqrt{3}}$
$\Rightarrow AC-\frac{AC}{\sqrt{3}} =BD$
$\Rightarrow AC\left( 1-\frac{1}{\sqrt{3}}\right) =100$
$\Rightarrow AC=\frac{100}{\left( 1-\frac{1}{\sqrt{3}}\right)}$
$=\frac{\left( 100\sqrt{3}\right)}{\left(\sqrt{3} -1\right)}$
$=236.98$ 米
因此，塔的高度為 236.98 米。
更新於： 2022年10月10日
705 次瀏覽
廣告