資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究梯形PQRS的對角線相交於點O，PQ∥RS且PQ = 3RS。求三角形POQ和ROS的面積比。
已知
梯形PQRS的對角線相交於點O，PQ∥RS且PQ = 3RS。
求解
我們需要求三角形POQ和ROS的面積比。
解答
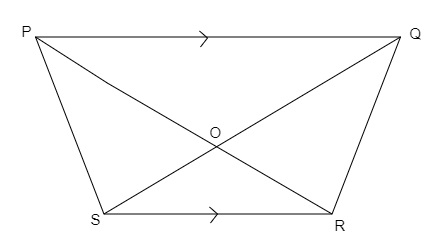
在三角形POQ和ROS中，
∠POQ=∠ROS (對頂角)
∠OPQ=∠ORS (因為PQ∥RS，內錯角相等)
因此，
△POQ ∽ △ROS (AA相似)
我們知道，
如果兩個三角形相似，則這兩個三角形的面積比等於它們對應邊長的平方比。
因此，
ar(△POQ)/ar(△ROS) = PQ²/RS²
=(3RS)²/RS²
=9RS²/RS²
=9/1
三角形POQ和ROS的面積比是9:1。
更新於：2022年10月10日
瀏覽量：103
廣告