兩個等邊三角形PQR和PQR'的底邊PQ位於y軸上，且PQ的中點位於原點，邊長為2a。求三角形的頂點R和R'的座標。

已知

兩個等邊三角形PQR和PQR'的底邊PQ位於y軸上，且PQ的中點位於原點。

要求

我們需要找到這兩個三角形的頂點R和R'的座標。

解答

△PQR和△PQR'是等邊三角形，每條邊長為2a，底邊為PQ，PQ的中點為O(0, 0)。PQ位於y軸上。

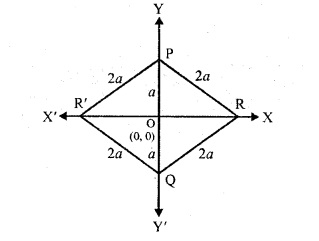
如圖所示，

PR=QR=PR'=QR'=2a PO=OQ=a

因此，

在直角三角形PRO中

PR²=PO²+OR² （勾股定理）

⇒(2a)²=(a)²+OR²

⇒4a²=a²+OR²

OR²=4a²-a²=3a²

∴OR=√3a

同樣地，

OR'=-√3a

因此，R的座標為(√3a, 0)，R'的座標為(-√3a, 0)。

教程點

更新於: 2022年10月10日

243次瀏覽

開啟你的職業生涯

完成課程獲得認證

立即開始