構造一個與給定三角形\( \triangle A B C \)相似的三角形，使其每條邊都是\( \triangle A B C \)對應邊的\( (2 / 3)^{\text {rd }} \)。已知\( B C=6 \mathrm{~cm}, \angle B=50^{\circ} \)和\( \angle C=60^{\circ} \)。
已知
一個三角形\( \triangle A B C \)，邊長\( B C=6 \mathrm{~cm}, \angle B=50^{\circ} \)和\( \angle C=60^{\circ} \)。
要求
我們必須構造一個與給定三角形\( \triangle A B C \)相似的三角形，使其每條邊都是\( \triangle A B C \)對應邊的\( (2 / 3)^{\text {rd }} \)。
解答
作圖步驟
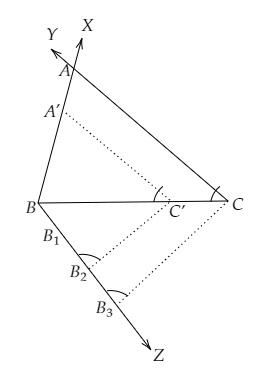
(i) 畫一條線段$BC = 6\ cm$。
(ii) 畫一條射線$BX$，與$BC$成$50^o$角，並畫另一條射線$CY$，與$BC$成$60^o$角，這兩條射線相交於點$A$。
$ABC$是所求三角形。
(iii) 從$B$點出發，畫另一條射線$BZ$，與$BC$在下方成一個銳角，並在射線上擷取三等分點，使得$BB_1 =B_1B_2 = B_2B_3$
(iv) 連線$B_3C$。
(v) 從$B_2$點出發，畫一條與$B_3C$平行的線段$B_2C^{’}$，並畫一條與$CA$平行的線段$C^{’}A^{’}$。
$A^{’}BC^{’}$是所求三角形。
相關文章 構造一個與給定三角形\( \triangle A B C \)相似的三角形，使其每條邊都是\( \triangle A B C \)對應邊的\( (5 / 7)^{\text {th }} \)。已知\( A B=5 \mathrm{~cm}, B C=7 \mathrm{~cm} \)和\( \angle A B C=50^{\circ} . \) 畫一個三角形\( \triangle A B C \)，其中邊長\( B C=6 \mathrm{~cm}, A B=5 \mathrm{~cm} \)和\( \angle A B C=60^{\circ} \)。然後，構造一個三角形，使其邊長是\( \triangle A B C \)對應邊長的\( (3 / 4)^{\text {th }} \)。 畫一個三角形\( \triangle A B C \)，其中底邊\( B C=6 \mathrm{~cm}, A B=5 \mathrm{~cm} \)和\( \angle A B C=60^{\circ} \)。然後構造另一個三角形，使其邊長是\( \triangle A B C \)對應邊長的\( \frac{3}{4} \)。 畫一個直角三角形\( A B C \)，其中\( A C=A B=4.5 \mathrm{~cm} \)和\( \angle A=90^{\circ} . \)畫一個與\( \triangle A B C \)相似的三角形，使其邊長是\( \triangle A B C \)對應邊長的\( (5 / 4) \)倍。 畫一個三角形\( \triangle A B C \)，其中\( B C=6 \mathrm{~cm}, A B=4 \mathrm{~cm} \)和\( A C=5 \mathrm{~cm} \)。畫一個與\( \triangle A B C \)相似的三角形，使其邊長是\( \triangle A B C \)對應邊長的\( (3 / 4)^{\text {th }} \)。 如果\( \triangle A B C \)是一個直角三角形，使得\( \angle C=90^{\circ}, \angle A=45^{\circ} \)和\( B C=7 \)個單位。求\( \angle B, A B \)和\( A C \)。 構造一個與\( \triangle A B C \)相似的三角形，其中\( A B=4.6 \mathrm{~cm}, \mathrm{BC}=5.1 \mathrm{~cm}, \angle A=60^{\circ} \)，比例因子為\( 4: 5 \)。 作一個$\triangle ABC$，其中$AB = 5\ cm, \angle B = 60^o$，高$CD = 3\ cm$。作一個與$\triangle ABC$相似的$\triangle AQR$，使得$\triangle AQR$的邊長是$\triangle ACB$對應邊長的1.5倍。 $\triangle A B C$是一個等腰三角形，使得$A B=A C$，$A D \perp B C$a) 證明$\triangle A B D \cong \triangle A C D$b) 證明$\angle B=\angle C$c) D是否是BC的中點？"\n \( \triangle \mathrm{ABC} \sim \triangle \mathrm{QPR} . \) 如果\( \angle \mathrm{A}+\angle \mathrm{B}=130^{\circ} \)和\( \angle B+\angle C=125^{\circ} \)，求\( \angle Q \)。 作一個等邊三角形，每邊長\( 5 \mathrm{~cm} \)。然後作另一個三角形，使其邊長是\( \triangle A B C \)對應邊長的\( 2 / 3 \)倍。 作一個邊長為\( 4 \mathrm{~cm}, 5 \mathrm{~cm} \)和\( 6 \mathrm{~cm} \)的三角形，然後作一個與它相似的三角形，使其邊長是它對應邊長的\( (2 / 3) \)倍。 如果給定三角形是等邊三角形，則$\angle ACD$的度數是多少？$( A).\ 60^{\circ}$$( B).\ 120^{\circ}$$( C).\ 180^{\circ}$$( D).\ 90^{\circ}$"\n 在一個直角三角形\( A B C \)中，\( C \)為直角，如果\( \angle B=60^{\circ} \)和\( A B=15 \)個單位。求其餘的角和邊。 在圖中，一個三角形\( \triangle A B C \)外接一個半徑為\( 4 \mathrm{~cm} \)的圓，使得線段\( B D \)和\( D C \)的長度分別為\( 8 \mathrm{~cm} \)和\( 6 \mathrm{~cm} \)。當\( \triangle A B C \)的面積為\( 84 \mathrm{~cm}^{2} \)時，求邊\( A B \)和\( A C \)的長度。"\n
資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究
