"\n">

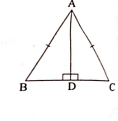
$\triangle ABC$ 是一個等腰三角形，其中 $AB=AC$，$AD \perp BC$
a) 證明 $\triangle ABD \cong \triangle ACD$
b) 證明 $\angle B=\angle C$ c) D 是 BC 的中點嗎？
"\n

已知

$AB = AC$

$AD$ 垂直於 $BC$。

需要證明

a) 證明 $\triangle ABD \cong \triangle ACD$

b) 證明 $\angle B=\angle C$

c) D 是 BC 的中點嗎？


解答


RHS 全等

在兩個直角三角形中，如果一個三角形的斜邊和一條邊的長度等於另一個三角形的斜邊和對應邊的長度，則這兩個三角形全等。

$AD$ 垂直於 $BC$。

$∠ADB = ∠ADC = 90°$

(a)

在 $△ABD$ 和 $△ACD$ 中，

$AB = AC$ (已知)

$AD = AD$ (公共邊)

$∠ADB = ∠ADC = 90°$

因此，根據 RHS 全等，

$△ABD ≅ △ACD$

證畢。

(b)

$△ABD ≅ △ACD$，

這意味著，

$∠ABD = ∠ACD$ (全等三角形對應角相等)

證畢。

(c)

$△ABD ≅ △ACD$，

這意味著，

$BD = DC$ (全等三角形對應邊相等)

因此，

D 是 BC 的中點。


更新於: 2022年10月10日

77 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習
廣告