資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
微軟 Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會研究
服裝研究
法律研究在下圖中，D 是邊 BC 的中點，且 AE ⊥ BC。如果 BC=a，AC=b，AB=c，ED=x，AD=p 且 AE=h，證明 b² + c² = 2p² + a²/2。
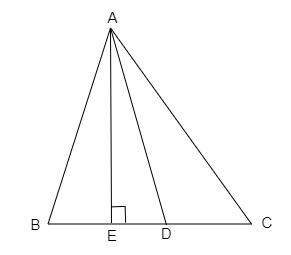
已知
在給定圖形中，D 是邊 BC 的中點，且 AE ⊥ BC。
BC=a，AC=b，AB=c，ED=x，AD=p 且 AE=h。
要求
我們必須證明 b² + c² = 2p² + a²/2。
解答
在△AED 中，根據勾股定理，
AD² = AE² + ED²
AE² = AD² - ED².....(i)
在△AEC 中，根據勾股定理，
AC² = AE² + EC² b² = (AD² - ED²) + (ED + DC)² (由 (i) 得)
b² = AD² - ED² + ED² + DC² + 2ED × DC
b² = AD² + DC² + 2DC × ED
b² = p² + (a/2)² + 2 × (a/2) × x (因為 DC = BC/2)
b² = p² + a²/4 + ax......(ii)
在△AEB 中，根據勾股定理，
AB² = AE² + BE²
c² = (AD² - ED²) + (BD - ED)² (由 (i) 和 BE = BD - ED 得)
c² = AD² - ED² + BD² + ED² - 2BD × ED
c² = AD² + BD² - 2BD × ED
c² = p² + (a/2)² - 2 × (a/2) × x (因為 DC = BC/2)
c² = p² + a²/4 - ax......(iii)
將方程 (ii) 和 (iii) 相加，我們得到：
b² + c² = p² + a²/4 + ax + p² + a²/4 - ax
b² + c² = 2p² + 2 × a²/4
b² + c² = 2p² + a²/2
證畢。
更新於：2022年10月10日
60 次瀏覽
廣告