在以\( C \)為直角的直角三角形\( \triangle A B C \)中，如果\( D \)是\( B C \)的中點，證明$B C^{2}=4(A D^{2}-A C^{2})$。

已知

在以\( C \)為直角的直角三角形\( \triangle A B C \)中，\( D \)是\( B C \)的中點。
需要做：

我們需要證明$B C^{2}=4(A D^{2}-A C^{2})$。

解答

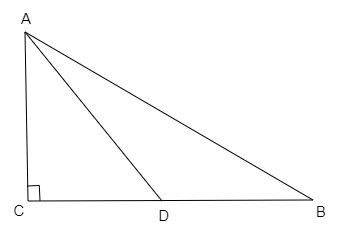
在$\triangle ADC$中，根據勾股定理，

$AD^2=AC^2+DC^2$

$DC^2=AD^2-AC^2$.....(i)

$BC=2DC$   (\( D \)是\( B C \)的中點)

$BC^2=(2DC)^2$

$BC^2=4DC^2$

$BC^2=4(AD^2-AC^2)$    (根據 (i))

證畢。

教程點

更新於: 2022年10月10日

68 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

立即開始