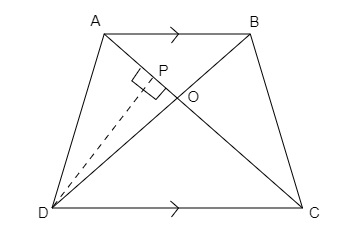
梯形ABCD中，AB∥CD。對角線AC和BD相交於點O。如果OA=6cm，OC=8cm，求△AOB面積與△COD面積的比值。

已知

ABCD是一個梯形，其中AB∥CD。對角線AC和BD相交於點O。

OA=6cm，OC=8cm。

要求

我們需要求出△AOB面積與△COD面積的比值。

解答

AB∥CD

在△AOB和△COD中，

∠AOB=∠COD (對頂角)

∠BAO=∠DCO (內錯角)

因此，

△AOB～△COD (根據角角相似)

我們知道，

如果兩個三角形相似，則這兩個三角形的面積之比等於它們對應邊長度之比的平方。

這意味著，

△AOB面積/△COD面積=OA²/OC²

=(6)²/(8)²

=36/64

=9/16

因此，

△AOB面積/△COD面積=9/16。

教程點

更新於: 2022年10月10日

69 次瀏覽

開啟你的職業生涯

透過完成課程獲得認證

開始學習