最大功率傳輸定理
最大功率傳輸定理 (MPT) 用於查詢負載電阻的值,在此值下,從電源到負載的功率傳輸量最大。
MPT 的陳述
連線到直流電源的電阻負載,當負載電阻等於從負載端子看到的電源的內部電阻時,接收到的功率最大。
MPT 的解釋
考慮以下電路圖,以確定 RL 的值,以便它從直流電源接收最大功率。

負載電流為:
$$I=\frac{V_{Th}}{R_{Th}+R_{L}}$$
因此,傳遞到電阻負載的功率為:
$$P_{L}=I^{2}R_{L}=(\frac{V_{Th}}{R_{Th}+R_{L}})^{2}R_{L}$$
眾所周知,負載電阻是可變的。因此,可以透過改變 RL 來最大化 PL。
$$\Rightarrow\:P_{L}=\frac{V_{Th}^{2}R_{L}}{(R_{th}+R_{L})^{2}}=\frac{V_{Th}^{2}R_{L}}{R_{Th}^{2}+R_{L}^{2}+2R_{Th}R_{L}}$$
$$\Rightarrow\:P_{L}=\frac{V_{Th}^{2}}{(\frac{R_{th}^{2}}{R_{L}}+R_{L}+2R_{Th})}=\frac{V_{Th}^{2}}{D}$$
為了使 PL 最大化,分母 (D) 項應最小,即:
$$\frac{dD}{dR_{L}}=0$$
$$\frac{d}{dR_{L}}(\frac{R_{Th}^{2}}{R_{L}}+R_{L}+2R_{Th})=0$$
透過求解上述微分方程,我們得到:
$$R_{L}=R_{Th}$$
因此,如果負載電阻等於源網路的內部電阻,則最大功率將傳遞到負載,即:
負載電阻 = 源的內部電阻
最大功率 (Pmax) 的量
$$P_{max}=\frac{V_{Th}^{2}}{4R_{Th}}$$
這裡,Pmax 是負載消耗的最大功率量。
電源提供的總功率為
$$P=2\frac{V_{Th}^{2}}{4R_{Th}}=\frac{V_{Th}^{2}}{2R_{Th}}$$
在最大功率傳輸期間電路的效率變為:
$$\eta=\frac{P_{max}}{P}\times\:100=50$$%
使用 MPT 求解網路的步驟
步驟 1 – 去除負載電阻,並將所有獨立電源替換為它們的內部電阻,並確定從開路負載端子觀察源網路的 RTh。
步驟 2 – 根據 MPT,RTh 的值給出負載電阻 RL 的值,即 RTh = RL,這允許最大功率傳輸。
步驟 3 – 找到開路負載端子上的 VTh 值。
步驟 4 – 傳輸的最大功率量由下式給出:
$$P_{max}=\frac{V_{Th}^{2}}{4R_{Th}}$$
數值示例
求下圖所示電路中負載電阻 RL 的值,使功率最大傳輸。並計算最大功率值。
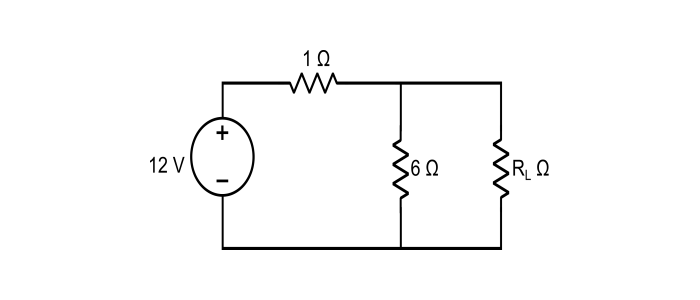
解決方案
步驟 1 – 去除負載電阻,並將所有獨立電源替換為它們的內部電阻(在本例中,12 V 理想電壓源短路),並確定給出與最大功率傳輸對應的 RL 的 RTh 值。
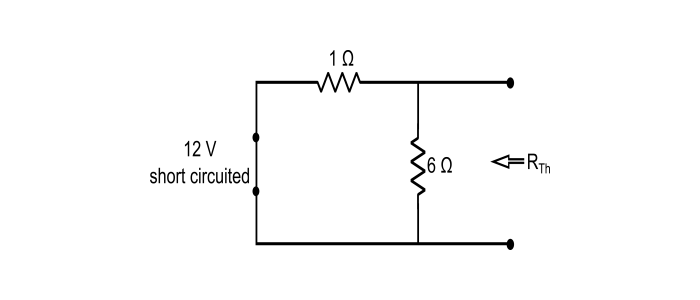
$$R_{Th}=1\:\Omega\:\lVert\:6\:\Omega=\frac{1\times\:6}{1+\:6}=\frac{6}{7}\:\Omega$$
根據最大功率傳輸定理:
$$R_{L}=R_{Th}=\frac{6}{7}\:\Omega$$
步驟 2 – 確定開路負載端子上的 VTh,
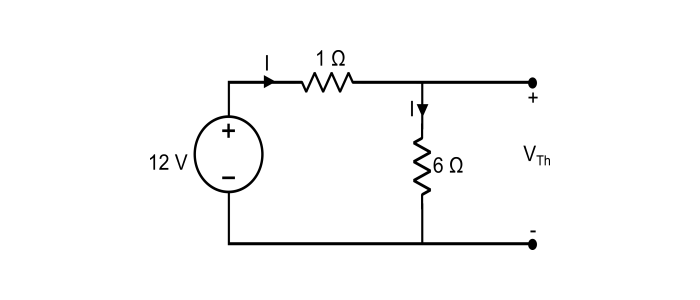
這裡,電路中的電流為:
$$I=\frac{12}{1+6}=\frac{12}{7}\:安培$$
由於負載端子是開路的,因此 VTh 是 6 Ω 電阻上的電壓降。因此,
$$V_{Th}=I\times\:6\Omega=\frac{12}{7}\times\:6=\frac{72}{7}\:伏特$$
傳遞到負載的最大功率量為:
$$P_{max}=\frac{V_{Th}^{2}}{4R_{Th}}=\frac{(72/7)^{2}}{4\times\:(6/7)}=30.857瓦特$$
因此,最大功率傳輸的負載電阻值為 (6/7 Ω),傳遞到負載的最大功率為 30.857 瓦特。


 資料結構
資料結構 網路
網路 關係型資料庫管理系統
關係型資料庫管理系統 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP