直流電機電壓方程、功率方程和最大機械功率條件
直流電機電壓方程
考慮圖中所示的直流並勵電機。

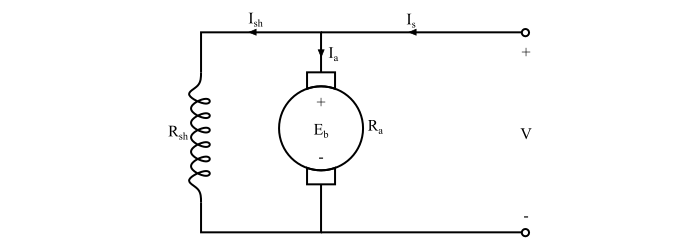
假設:
$$\mathrm{V\:=\:施加的直流電壓}$$
$$\mathrm{E_{b}\:=\:反電動勢}$$
$$\mathrm{R-{a} \:=\:電樞迴路電阻}$$
$$\mathrm{I_{a}\:=\:電樞電流}$$
在電樞迴路中應用基爾霍夫電壓定律,得到:
$$\mathrm{V\:=\:E_{b}\:+\:I_{a}R_{a} … (1)}$$
式 (1) 中的表示式稱為直流電機的電壓方程。
直流電機功率方程
如果在式 (1) 兩邊同時乘以 Ia,則得到:
$$\mathrm{VI_{a}\:=\:E_{b}I_{a}\:+\:I_a^2R_{a}\:.... (2)}$$
式 (2) 稱為直流電機的功率方程。忽略了機械損耗。
其中:
$$\mathrm{VI_{a}\:=\:輸入到電樞的電功率}$$
$$\mathrm{E_{b}I_{a}\:=\:電樞產生的機電功率}$$
$$\mathrm{I_a^2R_{a}\:=\:電樞銅損耗的電功率}$$
最大機械功率條件
電機產生的機械功率(忽略機械損耗)由下式給出:
$$\mathrm{P_{m}\:=\:E_{b}I_{a}}$$
$$\mathrm{⇒\:P_{m}\:= VI_{a}I_a^2R_{a}}$$
由於對於給定電機,V 和 Ra 是常數,因此電機產生的機械功率取決於電樞電流。
最大功率的條件由下式給出:
$$\mathrm{\frac{dP_{m}}{dI_{a}}\:=\:0}$$
$$\mathrm{\frac{d}{dI_{a}}(VI_{a}-I_a^2R_{a})\:=\:0}$$
$$\mathrm{⇒\:V\:-\:2I_{a}R_{a}\:=\:0}$$
$$\mathrm{⇒\:I_{a}R_{a\:=\:\frac{V}{2}}\:......(4)}$$
因此,
$$\mathrm{V\:=\:E_{b}\:+\:I_{a}R_{a}\:=\:E_{b}\:+\:\frac{V}{2}}$$
$$\mathrm{⇒E_{b}\:=\:\frac{V}{2}\:.....(5)}$$
因此,當反電動勢等於施加電壓的一半時,直流電機的機械功率最大。.


 資料結構
資料結構 網路
網路 關係資料庫管理系統
關係資料庫管理系統 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 程式設計
C 程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP