資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學同步電機輸出的機械功率
考慮一個欠勵磁（即 Ef < V）的三相圓柱轉子同步電機驅動機械負載。該圖顯示了電機的每相相量圖。由於電機欠勵磁，它將在滯後功率因數cos φ下執行。
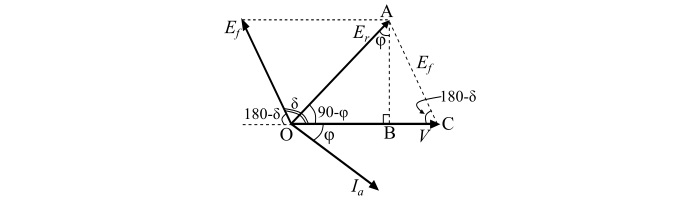
實際上，對於同步電機，XS>>Ra，因此可以忽略電機的電樞電阻 (Ra)。由於忽略了Ra，電樞銅損將為零。因此，同步電機輸出的機械功率 (Pm) 等於電機的輸入功率 (Pi)。
同樣，Ra= 0，Er=IaXS，因此電樞電流 (Ia) 滯後於合成電壓 (Er) 90°。
每相輸入功率：
$$\mathrm{P_{i}=V\:I_{a}\:cosφ}$$
因此，每相輸出的機械功率為：
$$\mathrm{P_{m}=P_{i}=V\:I_{a}\:Cosφ\:\:\:\:\:\:...(1)}$$
參考電機的相量圖，我們得到：
在三角形 ABO 中：
$$\mathrm{AB=E_{r}\:Cosφ=I_{a}X_{S}\:Cosφ}$$
並且，在三角形 ABC 中：
$$\mathrm{AB=E_{f}\:Sin(180°-δ)=E_{f}\:Sinδ}$$
$$\mathrm{\therefore\:I_{a}X_{S}\:Cosφ=E_{f}\:Sinδ}$$
$$\mathrm{\Longrightarrow\:I_{a}Cosφ=\frac{E_{f}}{X_{S}}\:Sinδ\:\:\:\:\:\:...(2)}$$
將 IaCosφ 的值代入公式 (1)，我們得到：
$$\mathrm{P_{m}=\frac{VE_{f}}{X_{S}}\:Sinδ\:\:\:\:\:\:...(3)}$$
公式 (3) 給出了同步電機每相輸出的機械功率。
三相總輸出的機械功率為：
$$\mathrm{P_{m}=\frac{3VE_{f}}{X_{S}}\:Sinδ\:\:\:\:\:\:...(4)}$$
最大機械功率輸出條件
對於同步電機的最大機械功率輸出：
$$\mathrm{\frac{dp_{m}}{dδ}=0\:and\:\frac{d^2p_{m}}{dδ^2}<0}$$
$$\mathrm{\Longrightarrow\:\frac{d}{dδ}\left [\frac{VE_{f}}{X_{S}}Sinδ\right ]=0}$$
$$\mathrm{\Longrightarrow\:\frac{VE_{f}}{X_{S}}\:Cosδ=0}$$
$$\mathrm{\Longrightarrow\:Cosδ=Cos90°}$$
$$\mathrm{\therefore\:δ=90°}$$
因此，當轉矩角等於 90°（電角度）時，輸出的機械功率最大。最大輸出功率由下式給出：
$$\mathrm{P_{m(max)}=\frac{VE_{f}}{X_{S}}...每相}$$
$$\mathrm{P_{m(max)}=\frac{3VE_{f}}{X_{S}}...總功率}$$
數值示例
一臺三相 5000 kW、11 kV、200 RPM、50 Hz 的同步電機，每相同步電抗為 1.5 Ω。在滿載時，電機的轉矩角為 23°（電角度）。如果勵磁電動勢為 3.4 kV，計算電機輸出的機械功率和最大機械功率。
解答
每相端電壓：
$$\mathrm{V=\frac{11000}{\sqrt{3}}=6351.04V}$$
輸出的機械功率：
$$\mathrm{P_{m}=\frac{3VE_{f}}{X_{S}}Sinδ=\frac{3\times6351.04\times3400}{1.5}\times\:Sin23°}$$
$$\mathrm{\Longrightarrow\:P_{m}=16.875 MW}$$
最大輸出機械功率為：
$$\mathrm{P_{m(max)}=\frac{3VE_{f}}{X_{S}}=\frac{3\times6351.04\times3400}{1.5}= 43.187 MW}$$
4K+ 次瀏覽
