資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究同步電動機的輸入功率是多少？
圖1和圖2分別顯示了滯後功率因數下的相量圖和圓柱形轉子同步電動機的等效電路圖。
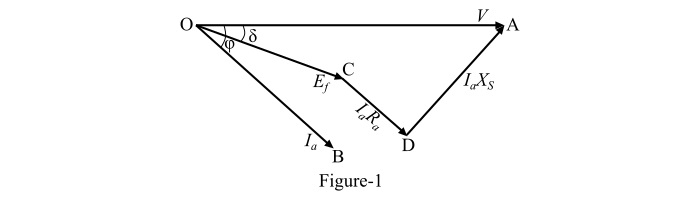
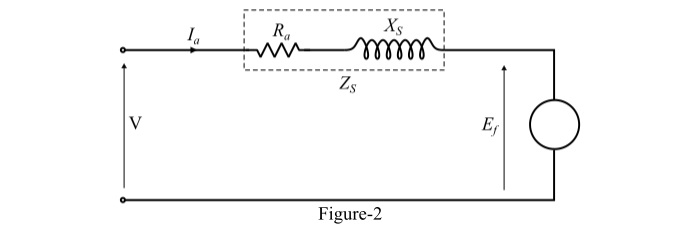
端電壓 (V) 作為參考相量，勵磁電壓 (Ef) 與端電壓 (V) 相差一個角度 δ，因此
$$\mathrm{V=V\angle0°\:and\:E_{f}=E_{f}\:\angle-δ}$$
在等效電路的迴路中應用基爾霍夫電壓定律 (KVL)，得到：
$$\mathrm{V=E_{f}+I_{a}Z_{S}\:\:\:\:\:\:...(1)}$$
$$\mathrm{\therefore\:I_{a}=\frac{V-E_{f}}{Z_{S}}\:\:\:\:\:\:...(2)}$$
$$\mathrm{\Longrightarrow\:I_{a}=\frac{V\angle0°-E_{f}\:\angle-δ}{Z_{S}\angleθ_{Z}}=\frac{V}{Z_{S}}\angle-θ_{Z}-\frac{E_{f}}{Z_{S}}\angle-(δ+θ_{Z})}$$
$$\mathrm{\therefore\:I^*_{a}=\frac{V}{Z_{S}}\angleθ_{Z}-\frac{E_{f}}{Z_{S}}\angle(δ+θ_{Z})\:\:\:\:\:\:...(3)}$$
因此，同步電動機的各種輸入功率表達式如下：
同步電動機每相的復功率輸入
同步電動機的復功率輸入由下式給出：
$$\mathrm{S_{i}=VI^*_{a}=P_{i}+jQ_{i}\:\:\:\:\:\:...(4)}$$
由公式 (3) 和 (4)，得到：
$$\mathrm{S_{i}=\frac{V^{2}}{Z_{S}}\angleθ_{Z}-\frac{VE_{f}}{Z_{S}}\angle(δ+θ_{Z})}$$
$$\mathrm{\Longrightarrow\:S_{i}=\left(\frac{V^{2}}{Z_{S}}cosθ_{Z}+j\frac{V^{2}}{Z_{S}}sinθ_{Z}\right)-\left(\frac{VE_{f}}{Z_{S}}cos(δ+θ_{Z})+j\frac{VE_{f}}{Z_{S}}sin(δ+θ_{Z})\right )}$$
$$\mathrm{\therefore\:S_{i}=\left[\frac{V^{2}}{Z_{S}}cosθ_{Z}-\frac{VE_{f}}{Z_{S}}cos(δ+θ_{Z})\right]+j\left[\frac{V^{2}}{Z_{S}}sinθ_{Z}-\frac{VE_{f}}{Z_{S}}sin(δ+θ_{Z})\right]\:\:\:\:\:\:...(5)}$$
同步電動機每相的實際輸入功率
透過計算公式 (5) 的第一項，可以得到同步電動機的有功功率輸入，即：
$$\mathrm{P_{i}=\frac{V^{2}}{Z_{S}}cosθ_{Z}-\frac{VE_{f}}{Z_{S}}cos(δ+θ_{Z})}$$
$$\mathrm{\because\:cosθ_{Z}=\frac{R_{a}}{Z_{S}}}$$
$$\mathrm{\therefore\:P_{i}=\frac{V^{2}}{Z^{2}_{S}}R_{a}-\frac{VE_{f}}{Z_{S}}cos(δ+θ_{Z})\:\:\:\:\:\:...(6)}$$
但是，
$$\mathrm{θ_{Z}=90°-α_{Z}}$$
$$\mathrm{cos(δ+θ_{Z})=cos(90°+δ-α_{Z})=-sin(δ-α_{Z})}$$
因此，同步電動機每相的有功功率輸入為：
$$\mathrm{P_{i}=\frac{V^{2}}{Z^{2}_{S}}R_{a}+\frac{VE_{f}}{Z_{S}}sin(δ-α_{Z})\:\:\:\:\:\:...(7)}$$
同步電動機每相的無功輸入功率
透過計算公式 (5) 的虛部（第二項），可以得到同步電動機的無功功率輸入值，即：
$$\mathrm{Q_{i}=\frac{V^{2}}{Z_{S}}sinθ_{Z}-\frac{VE_{f}}{Z_{S}}sin(δ+θ_{Z})}$$
$$\mathrm{\because\:sinθ_{Z}=\frac{X_{S}}{Z_{S}}}$$
$$\mathrm{\:Q_{i}=\frac{V^{2}}{Z^{2}_{S}}X_{S}-\frac{VE_{f}}{Z_{S}}sin(δ+θ_{Z})\:\:\:\:\:\:...(8)}$$
但是，
$$\mathrm{θ_{Z}=90°-α_{Z}}$$
$$\mathrm{sin(δ+θ_{Z})=sin(90°+δ-α_{Z})=cos(δ-α_{Z})}$$
因此，同步電動機的無功功率輸入為：
$$\mathrm{Q_{i}=\frac{V^{2}}{Z^{2}_{S}}X_{S}-\frac{VE_{f}}{Z_{S}}cos(δ-α_{Z})\:\:\:\:\:\:...(9)}$$
瀏覽量：588
