資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學同步發電機功率流傳遞方程
圖1顯示了圓柱轉子同步發電機的電路模型。
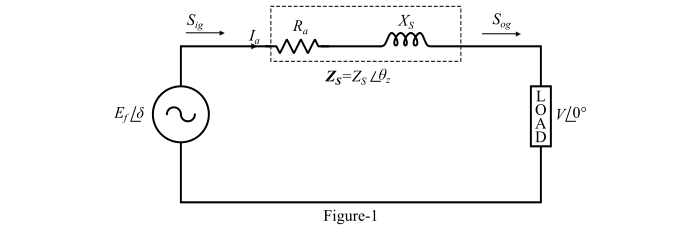
令：
𝑉 = 每相端電壓
$𝐸_{𝑓}$ = 每相勵磁電壓
$𝐼_{𝑎}$ = 電樞電流
$\delta$ = 負載角或𝑉和$𝐸_{𝑓}$之間的角度
此外，圖2顯示了滯後功率因數下交流發電機的相量圖。
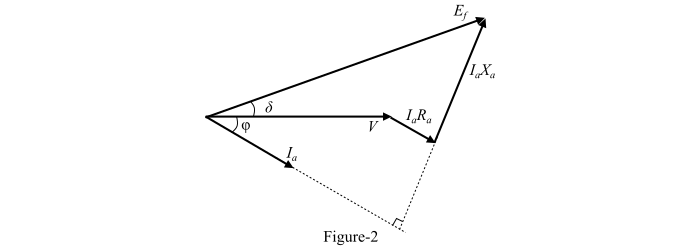
對於交流發電機或同步發電機，勵磁電壓($𝐸_{𝑓}$)以機器的負載角($\delta$)超前於端電壓(V)。因此，
$$\mathrm{𝑽 = 𝑉\angle0°\:\:and\:\:𝑬_{𝒇} = 𝐸_{𝑓}\angle \delta}$$
交流發電機的同步阻抗由下式給出：
$$\mathrm{𝒁_{𝒔} = 𝑅_{𝑎} + 𝑗𝑋_{𝑠} = 𝑍_{𝑠}\angle𝜃_{𝑧} … (1)}$$
其中，角度($𝜃_{𝑧}$)為阻抗角。
從圖3所示的阻抗三角形中，$𝜃_{𝑧}$由下式給出：
$$\mathrm{𝜃_{𝑧} = \tan^{-1} \left(\frac{𝑋_{𝑠}}{𝑅_{𝑎}} \right)… (2)}$$
並且
$$\mathrm{α_{𝑧} = (90° − 𝜃_{𝑧} ) = \tan^{-1} \left(\frac{𝑅_{𝑎}}{𝑋_{𝑠}} \right)… (3)}$$
現在，透過在圖1的電路中應用基爾霍夫電壓定律(KVL)，我們得到：
$$\mathrm{𝑬_{𝒇} = 𝑽 + 𝑰_{𝒂}𝒁_{𝒔} … (4)}$$
$$\mathrm{∴\:𝑰_{𝑎} =\frac{𝑬_{𝒇} − 𝑽}{𝒁_{𝒔}}… (5)}$$
交流發電機的功率流傳遞方程
考慮電樞電阻時，交流發電機的各種功率關係如下：
交流發電機每相的復功率輸出：
$$\mathrm{𝑆_{𝑜𝑔} = 𝑃_{𝑜𝑔} + 𝑗𝑄_{𝑜𝑔}}$$
$$\mathrm{=\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}cos(𝜃_{𝑧} − \delta) +𝑗\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}sin(𝜃_{𝑧} − \delta)-\frac{𝑉^{2}}{𝑍_{𝑠}}(cos\:𝜃_{𝑧} + 𝑗\:sin\:𝜃_{𝑧}) … (6)}$$
交流發電機每相的實際輸出功率：
$$\mathrm{𝑃_{𝑜𝑔}=\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}sin(\delta + α_{𝑧}) −\frac{𝑉^{2}}{𝑍^{2}_{𝑠}}𝑅_{𝑎} … (7)}$$
交流發電機每相的無功輸出功率：
$$\mathrm{𝑄_{𝑜𝑔} =\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}cos(\delta + α_{𝑧}) −\frac{𝑉^{2}}{𝑍^{2}_{𝑠}}𝑋_{𝑠} … (8)}$$
交流發電機每相的復功率輸入：
$$\mathrm{𝑆_{𝑖𝑔} = 𝑃_{𝑖𝑔} + 𝑗𝑄_{𝑖𝑔}}$$
$$\mathrm{=\frac{𝐸^{2}_{𝑓}}{𝑍_{𝑠}}(cos\:𝜃_{𝑧} + 𝑗\:sin\:𝜃_{𝑧}) −\left [\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}} cos(𝜃_{𝑧} + \delta) + 𝑗\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}sin(𝜃_{𝑧} + \delta )\right ]… (9)}$$
交流發電機每相的實際功率輸入：
$$\mathrm{𝑃_{𝑖𝑔} =\frac{𝐸^{2}_{𝑓}}{𝑍^{2}_{𝑠}}𝑅_{𝑎} +\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}sin(\delta − 𝛼_{𝑧} ) … (10)}$$
交流發電機每相的無功功率輸入：
$$\mathrm{𝑄_{𝑖𝑔} =\frac{𝐸^{2}_{𝑓}}{𝑍^{2}_{𝑠}}𝑋_{𝑠 }−\frac{𝑉𝐸_{𝑓}}{𝑍_{𝑠}}cos(\delta − α_{𝑧} ) … (11)}$$
忽略電樞電阻的交流發電機功率流方程
實際上，對於三相交流發電機或同步發電機，$𝑅_{𝑎}$ < $𝑋_{𝑠}$，因此在功率流傳遞方程中可以忽略電樞電阻($𝑅_{𝑎}$)。因此，當忽略電樞電阻($𝑅_{𝑎}$)時，同步阻抗為：
$$\mathrm{𝑍_{𝑠} = 𝑋_{𝑠}\:\:and\:\:α_{𝑧} = 0}$$
因此，交流發電機每相的輸出功率為：
$$\mathrm{𝑃_{𝑜𝑔} =\frac{𝑉𝐸_{𝑓}}{𝑋_{𝑠}}sin\:\delta … (12)}$$
$$\mathrm{𝑄_{𝑜𝑔} =\frac{𝑉𝐸_{𝑓}}{𝑋_{𝑠}}cos\:\delta −\frac{𝑉^{2}}{𝑋_{𝑠}}… (13)}$$
並且，交流發電機每相的輸入功率為：
$$\mathrm{𝑃_{𝑖𝑔} =\frac{𝑉𝐸_{𝑓}}{𝑋_{𝑠}}sin\:\delta = 𝑃_{𝑜𝑔} … (14)}$$
$$\mathrm{𝑄_{𝑖𝑔} =\frac{𝐸^{2}_{𝑓}}{𝑋_{𝑠}}−\frac{𝑉𝐸_{𝑓}}{𝑋_{𝑠}}cos\:\delta… (15)}$$
2K+ 次瀏覽
