資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會研究
服裝研究
法律研究同步發電機–零功率因數特性和Potier三角形
零功率因數特性(ZPFC)是當機器以同步速度和零滯後功率因數執行時，每相電樞端電壓和勵磁電流之間繪製的曲線圖。ZPFC也稱為Potier特性，以其創始人命名。
為了使功率因數保持非常低，交流發電機透過電抗器或欠勵磁同步電動機來載入。ZPFC的形狀非常類似於開路特性(O.C.C.)，向下和向右移動。
相量圖
圖1顯示了對應於零滯後功率因數負載的交流發電機的相量圖。
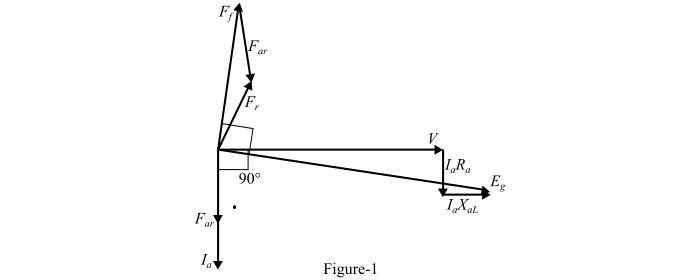
此處，每相端電壓(V)作為參考相量。在零滯後功率因數下，電樞電流(𝐼𝑎)滯後於電壓V 90°。電樞電阻中的電壓降(𝐼𝑎𝑅𝑎)與電流(𝐼𝑎)平行，洩漏電抗中的電壓降(𝐼𝑎𝑋𝑎𝐿)垂直於(𝐼𝑎)。
因此，每相產生的電壓為：
$$\mathrm{𝐸_{𝑔} = 𝑉 + 𝐼_{𝑎}𝑅_{𝑎} + 𝐼_{𝑎}𝑋_{𝑎L} … (1)}$$
如果
$𝐹_{𝑎𝑟}$ = 電樞反應磁勢(與$𝐼_{𝑎}$同相)
$𝐹_{𝑓}$ = 勵磁磁勢
$𝐹_{𝑟}$ = 氣隙中的合成磁勢
三個磁勢相量𝐹𝑓、𝐹𝑟和𝐹𝑎𝑟同相，其大小由以下等式關聯：
$$\mathrm{𝐹_{𝑓} = 𝐹_{𝑟} + 𝐹_{𝑎𝑟} … (2)}$$
如果忽略電樞電阻(𝑅𝑎)，則所得相量圖如圖2所示。從圖2可以看出，每相端電壓(V)、電抗電壓降(𝐼𝑎𝑋𝑎𝐿)和發電電壓(𝐸𝑔)都同相。因此，端電壓(V)實際上等於𝐸𝑔和𝐼𝑎𝑋𝑎𝐿的算術差，即：
$$\mathrm{𝑉 = 𝐸_{𝑔} − 𝐼_{𝑎}𝑋_{𝑎𝐿} … (3)}$$
公式(2)和(3)中給出的算術表示式構成了**Potier三角形**的基礎。
此外，公式(2)可以透過將兩邊除以轉子上的每極有效匝數(𝑇𝑓)轉換為等效勵磁電流形式。因此：
$$\mathrm{\frac{𝐹_{𝑓}}{𝑇_{𝑓}}=\frac{𝐹_{r}}{𝑇_{𝑓}}+\frac{𝐹_{𝑎𝑟}}{𝑇_{𝑓}}}$$
$$\mathrm{\Rightarrow\:𝐼_{𝑓} = 𝐼_{𝑟} + 𝐼_{𝑎𝑟} … (4)}$$
Potier三角形
圖3顯示了O.C.C.和ZPFC。
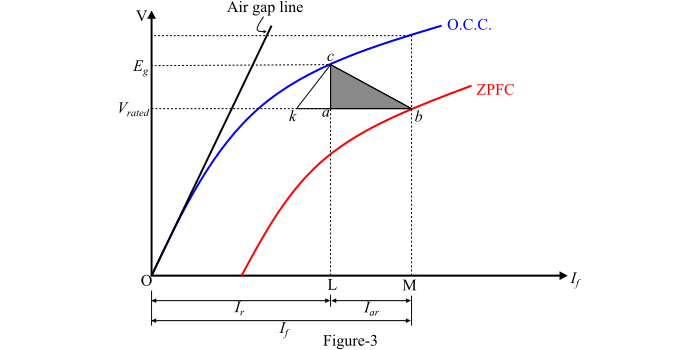
考慮ZPFC上一點b，對應於額定端電壓(V)和勵磁電流(𝑂𝑀 = 𝐼𝑓)。
如果在這種執行條件下，電樞反應磁勢(𝐹𝑎𝑟)的值以等效勵磁電流(𝐿𝑀 = 𝐼𝑎𝑟)表示，則合成磁勢(𝐹𝑟)的等效勵磁電流為(𝑂𝐿 = 𝐼𝑟)。
此合成勵磁電流(𝑂𝐿 = 𝐼𝑟)將根據O.C.C.產生髮電電壓(𝐿𝑐 = 𝐸𝑔)。由於對於零滯後功率因數執行，發電電壓由下式給出：
$$\mathrm{𝑬_{𝑔} = 𝑽 + 𝑰_{𝑎}𝑿_{𝑎𝐿} … (5)}$$
此處，垂直距離ac必須等於洩漏電抗電壓降(𝐼𝑎𝑋𝑎𝐿)，其中𝐼𝑎為額定電樞電流。因此，電樞洩漏電抗為：
$$\mathrm{𝑋_{𝑎𝐿} =\frac{每相電壓降𝑎𝑐}{額定電樞電流}… (6)}$$
現在，由頂點a、b和c形成的三角形稱為**Potier三角形**。
在同步電機中，勵磁漏磁通與電樞漏磁通的組合效應產生一個等效洩漏電抗𝑋𝑝，稱為**Potier電抗**。它由下式給出：
$$\mathrm{𝑋_{𝑝} =\frac{每相電壓降(電壓𝑎𝑐)}{零功率因數額定每相電樞電流(𝐼_{𝑎})}… (7)}$$
對於圓柱轉子同步電機，Potier電抗(𝑋𝑝)近似等於電樞洩漏電抗(𝑋𝑎𝐿)，而在凸極電機中，𝑋𝑝可能高達𝑋𝑎𝐿的3倍。
4K+ 次瀏覽
