迴歸演算法 - 線性迴歸

上一頁
下一頁

線性迴歸介紹

線性迴歸可以定義為分析因變數與一組給定自變數之間線性關係的統計模型。變數之間的線性關係意味著，當一個或多個自變數的值發生變化（增加或減少）時，因變數的值也會相應地發生變化（增加或減少）。

數學上，這種關係可以用以下等式表示：

Y = mX + b

這裡，Y是我們試圖預測的因變數

X 是我們用來進行預測的自變數。

m 是迴歸線的斜率，表示 X 對 Y 的影響

b 是一個常數，稱為 Y 截距。如果 X = 0，則 Y 等於 b。

此外，線性關係可以是正的或負的，如下所述：

正線性關係

如果自變數和因變數都增加，則線性關係稱為正線性關係。這可以透過下圖理解：

Positive Linear

負線性關係

如果自變數增加而因變數減少，則線性關係稱為負線性關係。這可以透過下圖理解：

Negative Linear

線性迴歸的型別

線性迴歸分為以下兩種型別：

  • 簡單線性迴歸
  • 多元線性迴歸

簡單線性迴歸 (SLR)

這是線性迴歸最基本的版本，它使用單個特徵來預測響應。SLR 的假設是這兩個變數之間存線上性關係。

Python 實現

我們可以透過兩種方式在 Python 中實現 SLR，一種是提供您自己的資料集，另一種是使用 scikit-learn Python 庫中的資料集。

示例 1 - 在下面的 Python 實現示例中，我們使用我們自己的資料集。

首先，我們將從匯入必要的包開始：

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

接下來，定義一個函式，該函式將計算 SLR 的重要值：

def coef_estimation(x, y):

以下指令碼行將給出觀察值的數量 n：

n = np.size(x)

x 和 y 向量的均值可以計算如下：

m_x, m_y = np.mean(x), np.mean(y)

我們可以找到關於 x 的交叉偏差和偏差：

SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_x

接下來，迴歸係數，即 b，可以計算如下：

b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)

接下來，我們需要定義一個函式，該函式將繪製迴歸線，並將預測響應向量：

def plot_regression_line(x, y, b):

以下指令碼行將實際點繪製為散點圖：

plt.scatter(x, y, color = "m", marker = "o", s = 30)

以下指令碼行將預測響應向量：

y_pred = b[0] + b[1]*x

以下指令碼行將繪製迴歸線並在其上放置標籤：

plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()

最後，我們需要定義 main() 函式來提供資料集並呼叫我們上面定義的函式：

def main():
   x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
   y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
   b = coef_estimation(x, y)
   print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
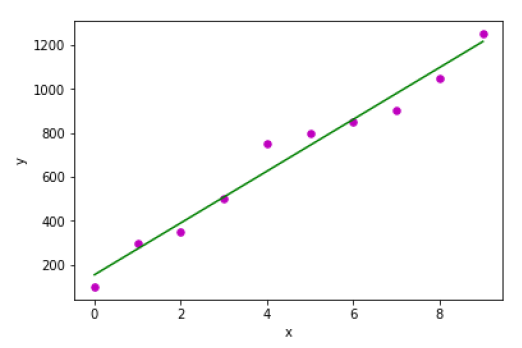
   plot_regression_line(x, y, b)
   
if __name__ == "__main__":
main()

輸出

Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788
Dataset

示例 2 - 在下面的 Python 實現示例中，我們使用 scikit-learn 的糖尿病資料集。

首先，我們將從匯入必要的包開始：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

接下來，我們將載入糖尿病資料集並建立其物件：

diabetes = datasets.load_diabetes()

由於我們正在實現 SLR，我們將只使用一個特徵：

X = diabetes.data[:, np.newaxis, 2]

接下來，我們需要將資料分割成訓練集和測試集：

X_train = X[:-30]
X_test = X[-30:]

接下來，我們需要將目標分割成訓練集和測試集：

y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]

現在，要訓練模型，我們需要建立一個線性迴歸物件：

regr = linear_model.LinearRegression()

接下來，使用訓練集訓練模型：

regr.fit(X_train, y_train)

接下來，使用測試集進行預測：

y_pred = regr.predict(X_test)

接下來，我們將列印一些係數，例如 MSE、方差分數等：

print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))

現在，繪製輸出：

plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

輸出

Coefficients:
   [941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
Red Blue

多元線性迴歸 (MLR)

它是簡單線性迴歸的擴充套件，它使用兩個或多個特徵來預測響應。數學上我們可以解釋如下：

考慮一個具有 n 個觀察值、p 個特徵（即自變數）和 y 作為單個響應（即因變數）的資料集，p 個特徵的迴歸線可以計算如下：

$$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}$$

這裡，h(xi) 是預測的響應值，b0,b1,b2…,bp 是迴歸係數。

多元線性迴歸模型總是包含資料中的誤差，稱為殘差誤差，這會改變計算結果：

$$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}+e_{i}$$

我們也可以將上述等式寫成：

$$y_{i}=h(x_{i})+e_{i}\:or\:e_{i}= y_{i} - h(x_{i})$$

Python 實現

在這個示例中，我們將使用 scikit-learn 的波士頓房價資料集：

首先，我們將從匯入必要的包開始：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics

接下來，載入資料集：

boston = datasets.load_boston(return_X_y=False)

以下指令碼行將定義特徵矩陣 X 和響應向量 Y：

X = boston.data
y = boston.target

接下來，將資料集分割成訓練集和測試集：

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)

示例

現在，建立線性迴歸物件並訓練模型：

reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
   color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
   color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
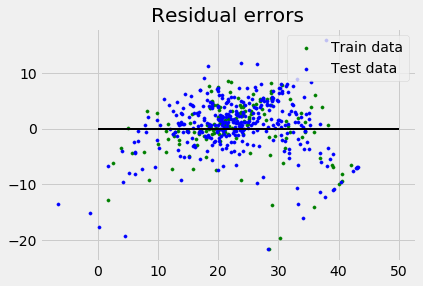
plt.title("Residual errors")
plt.show()

輸出

Coefficients:
[
   -1.16358797e-01  6.44549228e-02  1.65416147e-01  1.45101654e+00
   -1.77862563e+01  2.80392779e+00  4.61905315e-02 -1.13518865e+00
    3.31725870e-01 -1.01196059e-02 -9.94812678e-01  9.18522056e-03
   -7.92395217e-01
]
Variance score: 0.709454060230326
Spot

假設

以下是線性迴歸模型對資料集的一些假設：

多重共線性 - 線性迴歸模型假設資料中幾乎沒有或沒有多重共線性。基本上，當自變數或特徵之間存在依賴關係時，就會發生多重共線性。

自相關 - 線性迴歸模型的另一個假設是資料中幾乎沒有或沒有自相關。基本上，當殘差誤差之間存在依賴關係時，就會發生自相關。

變數之間的關係 - 線性迴歸模型假設響應變數和特徵變數之間的關係必須是線性的。

列印頁面
上一頁
下一頁
廣告