
- Python機器學習
- 首頁
- 基礎知識
- Python生態系統
- 機器學習方法
- 機器學習專案的資料載入
- 用統計學理解資料
- 用視覺化理解資料
- 資料準備
- 資料特徵選擇
- 機器學習演算法 - 分類
- 介紹
- 邏輯迴歸
- 支援向量機 (SVM)
- 決策樹
- 樸素貝葉斯
- 隨機森林
- 機器學習演算法 - 迴歸
- 隨機森林
- 線性迴歸
- 機器學習演算法 - 聚類
- 概述
- K均值演算法
- 均值漂移演算法
- 層次聚類
- 機器學習演算法 - KNN演算法
- 尋找最近鄰
- 效能指標
- 自動化工作流程
- 提升機器學習模型的效能
- 提升機器學習模型的效能(續…)
- Python機器學習 - 資源
- Python機器學習 - 快速指南
- Python機器學習 - 資源
- Python機器學習 - 討論
KNN演算法 - 尋找最近鄰
介紹
K近鄰(KNN)演算法是一種監督學習演算法,可用於分類和迴歸預測問題。然而,在工業中主要用於分類預測問題。以下兩個特性很好地定義了KNN:
懶惰學習演算法 - KNN是一種懶惰學習演算法,因為它沒有專門的訓練階段,並在分類時使用所有資料進行訓練。
非引數學習演算法 - KNN也是一種非引數學習演算法,因為它不對底層資料做任何假設。
KNN演算法的工作原理
K近鄰(KNN)演算法使用“特徵相似性”來預測新資料點的值,這意味著新資料點將根據其與訓練集中的點的匹配程度來分配值。我們可以透過以下步驟瞭解其工作原理:
步驟1 - 要實現任何演算法,我們需要資料集。因此,在KNN的第一步中,我們必須載入訓練資料和測試資料。
步驟2 - 接下來,我們需要選擇K的值,即最近的資料點。K可以是任何整數。
步驟3 - 對測試資料中的每個點執行以下操作:
3.1 - 使用歐幾里德距離、曼哈頓距離或漢明距離等方法計算測試資料與訓練資料每一行之間的距離。最常用的距離計算方法是歐幾里德距離。
3.2 - 現在,根據距離值,按升序對它們進行排序。
3.3 - 接下來,它將從排序陣列中選擇前K行。
3.4 - 現在,它將根據這些行的最頻繁類別為測試點分配一個類別。
步驟4 - 結束
示例
以下是一個示例,用於理解K的概念和KNN演算法的工作原理:
假設我們有一個可以繪製如下所示的資料集:
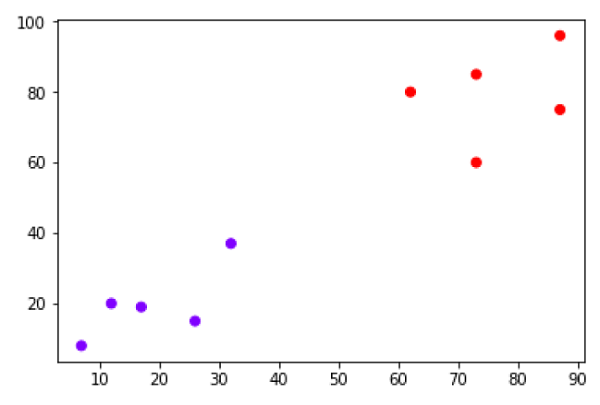
現在,我們需要將新的資料點(黑色點,位於點60,60)分類為藍色或紅色類別。我們假設K=3,即它將找到三個最近的資料點。這在下圖中顯示:
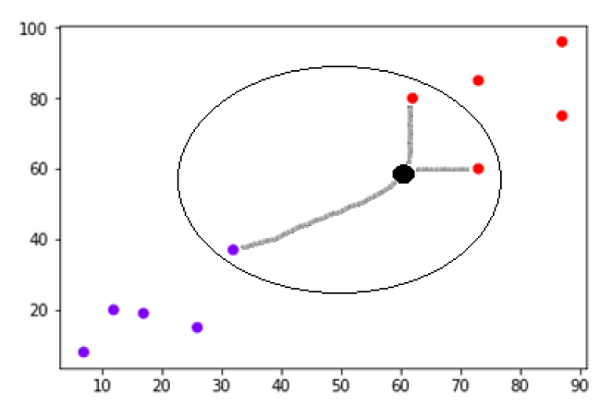
我們可以在上圖中看到黑色點資料的三個最近鄰。在這三個點中,有兩個屬於紅色類別,因此黑色點也將被分配到紅色類別。
Python實現
眾所周知,K近鄰(KNN)演算法可用於分類和迴歸。以下是使用KNN作為分類器和迴歸器的Python程式碼:
KNN作為分類器
首先,匯入必要的Python包:
import numpy as np import matplotlib.pyplot as plt import pandas as pd
接下來,從其網路連結下載鳶尾花資料集,如下所示:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
接下來,我們需要為資料集分配列名,如下所示:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
現在,我們需要將資料集讀取到pandas資料框中,如下所示:
dataset = pd.read_csv(path, names=headernames) dataset.head()
| 序號 | 萼片長度 | 萼片寬度 | 花瓣長度 | 花瓣寬度 | 類別 |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | Iris-setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | Iris-setosa |
資料預處理將使用以下指令碼行完成:
X = dataset.iloc[:, :-1].values y = dataset.iloc[:, 4].values
接下來,我們將資料劃分為訓練集和測試集。以下程式碼將資料集劃分為60%的訓練資料和40%的測試資料:
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40)
接下來,將進行資料縮放,如下所示:
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test)
接下來,使用sklearn的KNeighborsClassifier類訓練模型,如下所示:
from sklearn.neighbors import KNeighborsClassifier classifier = KNeighborsClassifier(n_neighbors=8) classifier.fit(X_train, y_train)
最後,我們需要進行預測。這可以透過以下指令碼完成:
y_pred = classifier.predict(X_test)
接下來,列印結果,如下所示:
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)
輸出
Confusion Matrix:
[[21 0 0]
[ 0 16 0]
[ 0 7 16]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 21
Iris-versicolor 0.70 1.00 0.82 16
Iris-virginica 1.00 0.70 0.82 23
micro avg 0.88 0.88 0.88 60
macro avg 0.90 0.90 0.88 60
weighted avg 0.92 0.88 0.88 60
Accuracy: 0.8833333333333333
KNN作為迴歸器
首先,匯入必要的Python包:
import numpy as np import pandas as pd
接下來,從其網路連結下載鳶尾花資料集,如下所示:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
接下來,我們需要為資料集分配列名,如下所示:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
現在,我們需要將資料集讀取到pandas資料框中,如下所示:
data = pd.read_csv(url, names=headernames) array = data.values X = array[:,:2] Y = array[:,2] data.shape output:(150, 5)
接下來,從sklearn匯入KNeighborsRegressor來擬合模型:
from sklearn.neighbors import KNeighborsRegressor knnr = KNeighborsRegressor(n_neighbors=10) knnr.fit(X, y)
最後,我們可以找到MSE,如下所示:
print ("The MSE is:",format(np.power(y-knnr.predict(X),2).mean()))
輸出
The MSE is: 0.12226666666666669
KNN的優缺點
優點
這是一個非常容易理解和解釋的演算法。
它對於非線性資料非常有用,因為該演算法不對資料做任何假設。
這是一個通用的演算法,因為我們可以將其用於分類和迴歸。
它具有相對較高的準確性,但比KNN更好的監督學習模型有很多。
缺點
它在計算上是一個比較昂貴的演算法,因為它儲存所有訓練資料。
與其他監督學習演算法相比,它需要較高的記憶體儲存。
如果N很大,預測速度會很慢。
它對資料的規模和不相關的特徵非常敏感。
KNN的應用
以下是KNN可以成功應用的一些領域:
銀行系統
KNN可用於銀行系統,以預測個人是否適合貸款審批?該個人是否具有與違約者相似的特徵?
計算信用評級
KNN演算法可用於透過與具有相似特徵的人進行比較來查找個人的信用評級。
政治
藉助KNN演算法,我們可以將潛在選民分類為不同的類別,例如“將投票”、“將不投票”、“將投票給國大黨”、“將投票給人民黨”。
KNN演算法還可以用於語音識別、手寫識別、影像識別和影片識別等其他領域。