分類 - 簡介

分類簡介

分類可以定義為從觀察值或給定資料點預測類別或範疇的過程。分類輸出可以採用“黑色”或“白色”或“垃圾郵件”或“非垃圾郵件”等形式。

在數學上，分類是從輸入變數 (X) 到輸出變數 (Y) 的近似對映函式 (f) 的任務。它基本上屬於監督機器學習，其中目標也與輸入資料集一起提供。

分類問題的示例可以是電子郵件中的垃圾郵件檢測。輸出只有兩種類別，“垃圾郵件”和“非垃圾郵件”；因此，這是一種二元分類。

為了實現這種分類，我們首先需要訓練分類器。對於此示例，“垃圾郵件”和“非垃圾郵件”電子郵件將用作訓練資料。成功訓練分類器後，它可用於檢測未知電子郵件。

分類中的學習器型別

在分類問題方面，我們有兩種型別的學習器 -

懶惰學習器

顧名思義，這種學習器在儲存訓練資料後等待測試資料出現。只有在獲得測試資料後才會進行分類。它們在訓練上花費的時間較少，但在預測上花費的時間較多。懶惰學習器的示例包括 K 最近鄰和基於案例的推理。

急切學習器

與懶惰學習器相反，急切學習器在儲存訓練資料後構建分類模型，而無需等待測試資料出現。它們在訓練上花費的時間更多，但在預測上花費的時間更少。急切學習器的示例包括決策樹、樸素貝葉斯和人工神經網路 (ANN)。

在 Python 中構建分類器

Scikit-learn 是一個用於機器學習的 Python 庫，可用於在 Python 中構建分類器。在 Python 中構建分類器的步驟如下 -

步驟 1：匯入必要的 Python 包

要使用 scikit-learn 構建分類器，我們需要匯入它。我們可以使用以下指令碼匯入它 -

import sklearn

步驟 2：匯入資料集

匯入必要的包後，我們需要一個數據集來構建分類預測模型。我們可以從 sklearn 資料集中匯入它，也可以根據我們的需要使用其他資料集。我們將使用 sklearn 的威斯康星州乳腺癌診斷資料庫。我們可以藉助以下指令碼匯入它 -

from sklearn.datasets import load_breast_cancer

以下指令碼將載入資料集；

data = load_breast_cancer()

我們還需要整理資料，這可以透過以下指令碼完成 -

label_names = data['target_names']
   labels = data['target']
   feature_names = data['feature_names']
   features = data['data']

以下命令將列印標籤的名稱，在我們的資料庫情況下為“惡性”和“良性”。

print(label_names)

上述命令的輸出是標籤的名稱 -

['malignant' 'benign']

這些標籤對映到二進位制值 0 和 1。惡性癌症由 0 表示，良性癌症由 1 表示。

這些標籤的特徵名稱和特徵值可以透過以下命令檢視 -

print(feature_names[0])

上述命令的輸出是標籤 0 即惡性癌症的特徵名稱 -

mean radius

類似地，標籤的特徵名稱可以如下生成 -

print(feature_names[1])

上述命令的輸出是標籤 1 即良性癌症的特徵名稱 -

mean texture

我們可以透過以下命令列印這些標籤的特徵 -

print(features[0])

這將給出以下輸出 -

[
   1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
   1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
   6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
   1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
   4.601e-01 1.189e-01
]

我們可以透過以下命令列印這些標籤的特徵 -

print(features[1])

這將給出以下輸出 -

[
   2.057e+01 1.777e+01 1.329e+02 1.326e+03 8.474e-02 7.864e-02 8.690e-02
   7.017e-02 1.812e-01 5.667e-02 5.435e-01 7.339e-01 3.398e+00 7.408e+01
   5.225e-03 1.308e-02 1.860e-02 1.340e-02 1.389e-02 3.532e-03 2.499e+01
   2.341e+01 1.588e+02 1.956e+03 1.238e-01 1.866e-01 2.416e-01 1.860e-01
   2.750e-01 8.902e-02
]

步驟 3：將資料組織成訓練集和測試集

由於我們需要在未見過的資料上測試我們的模型，因此我們將資料集分成兩部分：訓練集和測試集。我們可以使用 sklearn python 包的 train_test_split() 函式將資料拆分為資料集。以下命令將匯入該函式 -

from sklearn.model_selection import train_test_split

現在，下一個命令將資料拆分為訓練資料和測試資料。在此示例中，我們使用 40% 的資料進行測試，60% 的資料進行訓練 -

train, test, train_labels, test_labels = train_test_split(
   features,labels,test_size = 0.40, random_state = 42
)

步驟 4：模型評估

將資料分成訓練集和測試集後，我們需要構建模型。我們將使用樸素貝葉斯演算法來實現此目的。以下命令將匯入 GaussianNB 模組 -

from sklearn.naive_bayes import GaussianNB

現在，初始化模型如下 -

gnb = GaussianNB()

接下來，藉助以下命令，我們可以訓練模型 -

model = gnb.fit(train, train_labels)

現在，出於評估目的，我們需要進行預測。這可以透過使用 predict() 函式來完成，如下所示 -

preds = gnb.predict(test)
print(preds)

這將給出以下輸出 -

[
   1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1
   0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1
   1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0
   0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1
   1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 
   1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 
   1

]

輸出中的 0 和 1 的上述序列是惡性和良性腫瘤類別的預測值。

步驟 5：查詢準確率

我們可以透過比較兩個陣列（即 test_labels 和 preds）來找到上一步中構建的模型的準確率。我們將使用 accuracy_score() 函式來確定準確率。

from sklearn.metrics import accuracy_score
   print(accuracy_score(test_labels,preds))
   0.951754385965

上述輸出表明樸素貝葉斯分類器的準確率為 95.17%。

分類評估指標

即使您完成了機器學習應用程式或模型的實施，工作也尚未完成。我們必須找出我們的模型有多有效？可能有不同的評估指標，但我們必須仔細選擇它，因為指標的選擇會影響如何衡量和比較機器學習演算法的效能。

以下是您可以根據您的資料集和問題型別選擇的幾個重要的分類評估指標 -

混淆矩陣

這是衡量分類問題效能的最簡單方法，其中輸出可以是兩種或多種型別的類別。混淆矩陣不過是一個二維表，即“實際”和“預測”，此外，這兩個維度都有“真陽性 (TP)”、“真陰性 (TN)”、“假陽性 (FP)”、“假陰性 (FN)”如下所示 -

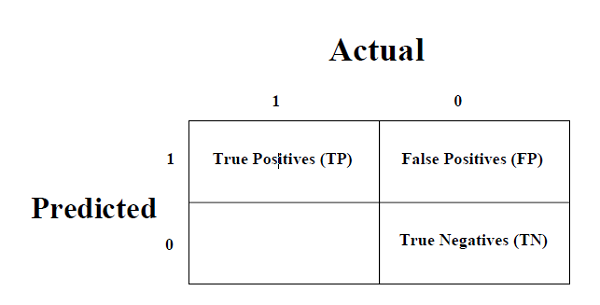
與混淆矩陣相關的術語的解釋如下 -

**真陽性 (TP)** - 資料點的實際類別和預測類別均為 1 的情況。
**真陰性 (TN)** - 資料點的實際類別和預測類別均為 0 的情況。
**假陽性 (FP)** - 資料點的實際類別為 0，預測類別為 1 的情況。
**假陰性 (FN)** - 資料點的實際類別為 1，預測類別為 0 的情況。

我們可以藉助 sklearn 的 confusion_matrix() 函式找到混淆矩陣。藉助以下指令碼，我們可以找到上面構建的二元分類器的混淆矩陣 -

from sklearn.metrics import confusion_matrix

輸出

[
   [ 73   7]
   [  4 144]
]

準確率

可以將其定義為我們的機器學習模型做出的正確預測的數量。我們可以很容易地透過以下公式用混淆矩陣計算它 -

$$𝐴𝑐𝑐𝑢𝑟𝑎𝑐𝑦=\frac{𝑇𝑃+𝑇𝑁}{𝑇𝑃+𝐹𝑃+𝐹𝑁+𝑇𝑁}$$

對於上面構建的二元分類器，TP + TN = 73 + 144 = 217 且 TP + FP + FN + TN = 73 + 7 + 4 + 144 = 228。

因此，準確率 = 217/228 = 0.951754385965，與我們在建立二元分類器後計算的結果相同。

精確率

精確率，用於文件檢索，可以定義為我們的機器學習模型返回的正確文件的數量。我們可以很容易地透過以下公式用混淆矩陣計算它 -

$$𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛=\frac{𝑇𝑃}{𝑇𝑃+FP}$$

對於上面構建的二元分類器，TP = 73 且 TP + FP = 73 + 7 = 80。

因此，精確率 = 73/80 = 0.915

召回率或靈敏度

召回率可以定義為我們的機器學習模型返回的陽性數量。我們可以很容易地透過以下公式用混淆矩陣計算它 -

$$𝑅𝑒𝑐𝑎𝑙𝑙=\frac{𝑇𝑃}{𝑇𝑃+FN}$$

對於上面構建的二元分類器，TP = 73 且 TP + FN = 73 + 4 = 77。

因此，精確率 = 73/77 = 0.94805

特異性

與召回率相反，特異性可以定義為我們的機器學習模型返回的陰性數量。我們可以很容易地透過以下公式用混淆矩陣計算它 -

$$𝑆𝑝𝑒𝑐𝑖𝑓𝑖𝑐𝑖𝑡𝑦=\frac{𝑇N}{𝑇N+FP}$$

對於上面構建的二元分類器，TN = 144 且 TN + FP = 144 + 7 = 151。

因此，精確率 = 144/151 = 0.95364

各種機器學習分類演算法

以下是幾個重要的機器學習分類演算法 -

邏輯迴歸
支援向量機 (SVM)
決策樹
樸素貝葉斯
隨機森林

我們將在後面的章節中詳細討論所有這些分類演算法。

應用

以下是分類演算法的一些最重要的應用 -

語音識別
手寫識別
生物識別身份識別
文件分類

列印頁面