支援向量機 (SVM)

上一頁
下一頁

SVM簡介

支援向量機（SVM）是一種功能強大且靈活的監督式機器學習演算法，可用於分類和迴歸。但通常，它們用於分類問題。SVM最早在20世紀60年代被提出，但在20世紀90年代得到了完善。與其他機器學習演算法相比，SVM有其獨特的實現方式。最近，由於其能夠處理多個連續和分類變數，因此它們非常受歡迎。

SVM的工作原理

SVM模型基本上是在多維空間中超平面中不同類的表示。超平面將以迭代方式由SVM生成，以便最大程度地減少錯誤。SVM的目標是將資料集劃分為不同的類別以找到最大間隔超平面（MMH）。

Margin

以下是在SVM中重要的概念：

  • 支援向量 - 最接近超平面的資料點稱為支援向量。分離線將藉助這些資料點來定義。

  • 超平面 - 正如我們在上圖中看到的，它是一個決策平面或空間，它將一組具有不同類別的物件劃分開來。

  • 間隔 - 可以定義為不同類別的最近資料點之間的兩條線之間的間隙。它可以計算為從線到支援向量的垂直距離。大的間隔被認為是好的間隔，而小的間隔被認為是壞的間隔。

SVM的主要目標是將資料集劃分為不同的類別以找到最大間隔超平面（MMH），這可以透過以下兩個步驟完成：

  • 首先，SVM將迭代地生成超平面，以最佳方式分離類別。

  • 然後，它將選擇正確分離類別的超平面。

在Python中實現SVM

為了在Python中實現SVM，我們將從匯入標準庫開始，如下所示：

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns; sns.set()

接下來，我們正在建立一個示例資料集，該資料集具有線性可分離的資料，來自sklearn.dataset.sample_generator，用於使用SVM進行分類：

from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=100, centers=2, random_state=0, cluster_std=0.50)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');

生成包含100個樣本和2個聚類的樣本資料集後的輸出如下所示：

Map

我們知道SVM支援判別式分類。它透過簡單地在二維情況下找到一條線或在多維情況下找到一個流形來將類別彼此分開。它在上述資料集上實現如下：

xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
plt.plot([0.6], [2.1], 'x', color='black', markeredgewidth=4, markersize=12)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
   plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5);

輸出如下：

Cross

從上面的輸出中我們可以看到，有三個不同的分離器可以完美地區分上述樣本。

如上所述，SVM的主要目標是將資料集劃分為不同的類別以找到最大間隔超平面（MMH），因此，而不是在類別之間繪製零線，我們可以在每條線的周圍繪製一定寬度的間隔，直到最近的點。這可以透過以下方式完成：

xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
   for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
   yfit = m * xfit + b
   plt.plot(xfit, yfit, '-k')
   plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
         color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
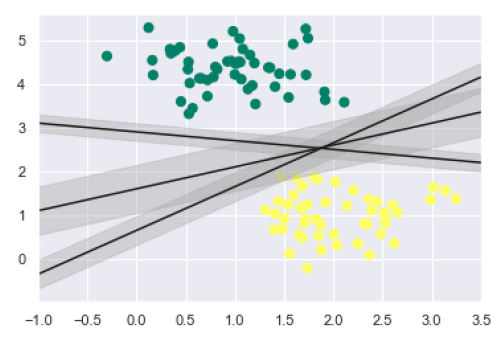
Green

從輸出中的上圖中，我們可以很容易地觀察到判別分類器內的“間隔”。SVM將選擇最大化間隔的線。

接下來，我們將使用Scikit-Learn的支援向量分類器在這個資料上訓練一個SVM模型。在這裡，我們使用線性核來擬合SVM，如下所示：

from sklearn.svm import SVC # "Support vector classifier"
model = SVC(kernel='linear', C=1E10)
model.fit(X, y)

輸出如下：

SVC(C=10000000000.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)

現在，為了更好地理解，以下將繪製二維SVC的決策函式：

def decision_function(model, ax=None, plot_support=True):
   if ax is None:
      ax = plt.gca()
   xlim = ax.get_xlim()
   ylim = ax.get_ylim()

為了評估模型，我們需要建立網格，如下所示：

x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)

接下來，我們需要繪製決策邊界和間隔，如下所示：

ax.contour(X, Y, P, colors='k',
   levels=[-1, 0, 1], alpha=0.5,
   linestyles=['--', '-', '--'])

現在，類似地繪製支援向量，如下所示：

if plot_support:
   ax.scatter(model.support_vectors_[:, 0],
      model.support_vectors_[:, 1],
      s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)

現在，使用此函式擬合我們的模型，如下所示：

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
decision_function(model);
Yellow

從上面的輸出中我們可以觀察到，一個SVM分類器擬合了具有間隔（即虛線）和支援向量的資料，這些支援向量是此擬合的關鍵元素，接觸到虛線。這些支援向量點儲存在分類器的support_vectors_屬性中，如下所示：

model.support_vectors_

輸出如下：

array([[0.5323772 , 3.31338909],
   [2.11114739, 3.57660449],
   [1.46870582, 1.86947425]])

SVM核函式

在實踐中，SVM演算法是用核函式實現的，該核函式將輸入資料空間轉換為所需的形式。SVM使用一種稱為核技巧的技術，其中核函式採用低維輸入空間並將其轉換為高維空間。簡單來說，核函式透過向其中新增更多維度將不可分離問題轉換為可分離問題。它使SVM更加強大、靈活和準確。以下是SVM使用的一些核函式型別：

線性核函式

它可以用作任何兩個觀測值之間的點積。線性核函式的公式如下所示：

k(x,xi) = sum(x*xi)

從上面的公式中，我們可以看到兩個向量（例如𝑥和𝑥𝑖）之間的乘積是每對輸入值的乘積之和。

多項式核函式

它是線性核函式的更一般形式，可以區分曲線或非線性輸入空間。以下是多項式核函式的公式：

K(x, xi) = 1 + sum(x * xi)^d

這裡d是多項式的次數，我們需要在學習演算法中手動指定它。

徑向基函式 (RBF) 核函式

RBF核函式主要用於SVM分類，它將輸入空間對映到無限維空間。以下公式在數學上解釋了它：

K(x,xi) = exp(-gamma * sum((x – xi^2))

這裡，gamma的範圍是0到1。我們需要在學習演算法中手動指定它。gamma的一個好的預設值是0.1。

由於我們為線性可分離資料實現了SVM，因此我們可以使用核函式在Python中為不可分離資料實現它。

示例

以下是使用核函式建立SVM分類器的示例。我們將使用來自scikit-learn的鳶尾花資料集：

我們將從匯入以下包開始：

import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as plt

現在，我們需要載入輸入資料：

iris = datasets.load_iris()

從此資料集中，我們獲取前兩個特徵，如下所示：

X = iris.data[:, :2]
y = iris.target

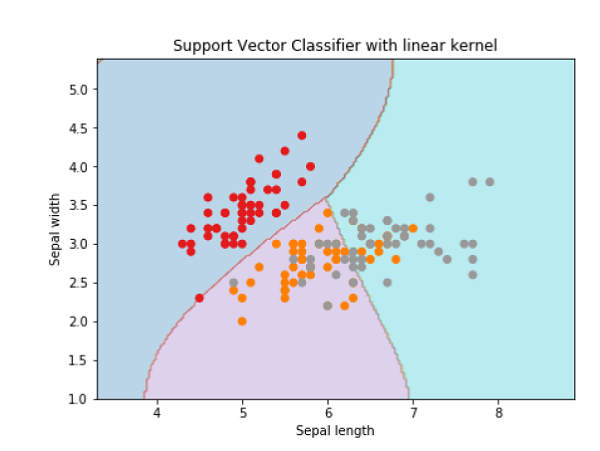
接下來，我們將使用原始資料繪製SVM邊界，如下所示：

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
   np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]

現在，我們需要提供正則化引數的值，如下所示：

C = 1.0

接下來，可以建立SVM分類器物件，如下所示：

Svc_classifier = svm.SVC(kernel='linear', C=C).fit(X, y)

Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with linear kernel')

輸出

Text(0.5, 1.0, 'Support Vector Classifier with linear kernel')
Curve

為了使用rbf核建立SVM分類器，我們可以將核函式更改為rbf，如下所示：

Svc_classifier = svm.SVC(kernel='rbf', gamma =‘auto’,C=C).fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with rbf kernel')

輸出

Text(0.5, 1.0, 'Support Vector Classifier with rbf kernel')
Classifier

我們將gamma的值設定為'auto'，但您也可以提供其值（0到1之間）。

SVM分類器的優缺點

SVM分類器的優點

SVM分類器提供很高的準確性，並且在高維空間中表現良好。SVM分類器基本上使用訓練點的一個子集，因此結果使用非常少的記憶體。

SVM分類器的缺點

它們的訓練時間很長，因此在實踐中不適合大型資料集。另一個缺點是SVM分類器在處理重疊類別時效果不佳。

列印頁面
上一頁
下一頁
廣告