聚類演算法 - K均值演算法

上一頁
下一頁

K均值演算法介紹

K均值聚類演算法計算質心並迭代，直到找到最佳質心。它假設聚類的數量已知。它也稱為平面聚類演算法。演算法從資料中識別出的聚類數量用K均值中的“K”表示。

在此演算法中，資料點被分配到一個聚類，使得資料點和質心之間平方距離之和最小。需要理解的是，聚類內部的方差越小，同一聚類內的資料點就越相似。

K均值演算法的工作原理

我們可以透過以下步驟瞭解K均值聚類演算法的工作原理：

  • 步驟1 - 首先，我們需要指定此演算法需要生成的聚類數量K。

  • 步驟2 - 接下來，隨機選擇K個數據點並將每個資料點分配給一個聚類。簡單來說，就是根據資料點的數量對資料進行分類。

  • 步驟3 - 現在它將計算聚類質心。

  • 步驟4 - 接下來，繼續迭代以下步驟，直到我們找到最佳質心，即資料點到聚類的分配不再發生變化：

4.1 - 首先，計算資料點和質心之間平方距離之和。

4.2 - 現在，我們必須將每個資料點分配到比其他聚類（質心）更接近的聚類。

4.3 - 最後，透過取該聚類中所有資料點的平均值來計算聚類的質心。

K均值採用期望最大化方法來解決問題。期望步驟用於將資料點分配給最近的聚類，最大化步驟用於計算每個聚類的質心。

使用K均值演算法時，需要注意以下幾點：

  • 在使用包括K均值在內的聚類演算法時，建議標準化資料，因為此類演算法使用基於距離的度量來確定資料點之間的相似性。

  • 由於K均值的迭代性質和質心的隨機初始化，K均值可能會停留在區域性最優，而可能無法收斂到全域性最優。因此，建議使用不同的質心初始化。

Python實現

以下兩個實現K均值聚類演算法的示例將幫助我們更好地理解它：

示例1

這是一個簡單的例子，用於理解K均值的工作原理。在這個例子中，我們將首先生成一個包含4個不同blob的二維資料集，然後應用K均值演算法來檢視結果。

首先，我們將從匯入必要的包開始：

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

以下程式碼將生成包含四個blob的二維資料集：

from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)

接下來，以下程式碼將幫助我們視覺化資料集：

plt.scatter(X[:, 0], X[:, 1], s=20);
plt.show()
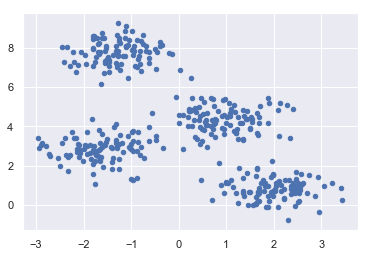
World Map

接下來，建立一個KMeans物件，同時提供聚類數量，訓練模型並進行預測，如下所示：

kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)

現在，藉助以下程式碼，我們可以繪製並可視化K均值Python估計器選擇的聚類中心：

plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=20, cmap='summer')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='blue', s=100, alpha=0.9);
plt.show()
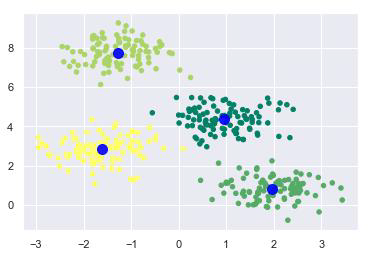
World Spot

示例2

讓我們來看另一個例子，我們將對簡單的數字資料集應用K均值聚類。K均值將嘗試在不使用原始標籤資訊的情況下識別相似的數字。

首先，我們將從匯入必要的包開始：

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

接下來，從sklearn載入數字資料集並建立它的物件。我們還可以找到此資料集中行數和列數，如下所示：

from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape

輸出

(1797, 64)

上面的輸出顯示，此資料集有1797個樣本，具有64個特徵。

我們可以像在上面的示例1中一樣執行聚類：

kmeans = KMeans(n_clusters=10, random_state=0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape

輸出

(10, 64)

上面的輸出顯示，K均值建立了10個具有64個特徵的聚類。

fig, ax = plt.subplots(2, 5, figsize=(8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
   axi.set(xticks=[], yticks=[])
   axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)

輸出

作為輸出，我們將獲得以下影像，顯示K均值學習的聚類中心。

Blur

以下幾行程式碼將學習到的聚類標籤與其中找到的真實標籤匹配：

from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
   mask = (clusters == i)
   labels[mask] = mode(digits.target[mask])[0]

接下來，我們可以檢查準確性，如下所示：

from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)

輸出

0.7935447968836951

上面的輸出顯示準確率約為80%。

優點和缺點

優點

以下是K均值聚類演算法的一些優點：

  • 它很容易理解和實現。

  • 如果我們有很多變數，那麼K均值將比層次聚類更快。

  • 重新計算質心時，例項可以更改聚類。

  • 與層次聚類相比，K均值形成更緊密的聚類。

缺點

以下是K均值聚類演算法的一些缺點：

  • 很難預測聚類的數量，即k的值。

  • 輸出受到初始輸入（如聚類數量（k的值））的強烈影響。

  • 資料的順序將對最終輸出產生強烈影響。

  • 它對重新縮放非常敏感。如果我們透過歸一化或標準化來重新縮放資料，則輸出將完全改變。最終輸出。

  • 如果聚類具有複雜的幾何形狀，它在聚類方面表現不佳。

K均值聚類演算法的應用

聚類分析的主要目標是：

  • 從我們正在使用的資料中獲得有意義的直覺。

  • 先聚類後預測，其中將為不同的子組構建不同的模型。

為了實現上述目標，K均值聚類表現足夠好。它可用於以下應用：

  • 市場細分

  • 文件聚類

  • 影像分割

  • 影像壓縮

  • 客戶細分

  • 分析動態資料的趨勢

列印頁面
上一頁
下一頁
廣告