功-能定理的推導

---

簡介

功-能定理指出，外力對物體所做的淨功等於該物體動能的變化率。功-能定理指的是所有作用在物體上的力的功，而不是單個力的功。根據功-能定理，動能被定義為將物體從靜止狀態加速到所需速度所需的功。

什麼是功-能定理？

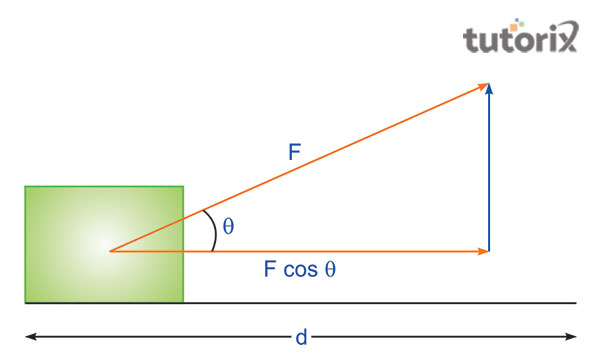
圖 1：功-能定理示意圖

功-能定理的公式表示為 W= FdcosӨ，其中 W 表示功，F 表示作用在物體上導致其從初始位置發生位移的外力，d 表示物體兩個不同位置之間的距離。物體由於所具有的能量而產生的運動稱為動能。

功-能定理的推導

根據運動學公式，功-能定理的推導可以定義為 v² = u² + 2as，其中 V 表示物體的最終速度，u 表示物體的初始速度，a 表示恆定加速度，s 表示物體的位移。

根據牛頓第二定律 F = ma，因此該公式也可以寫成 1/2 mv² - 1/2 mu² = F.d

這裡，W 等於 F.d，而 K.E. 等於 (mv²)/2，則公式可以表示為 K_f – K_i = W。

因此，ΔK = W，其中 ΔK 表示 Kf – Ki，即動能的變化。

所以，可以說對特定物體所做的功等於其動能的變化。

變力下的功-能定理

日常生活中常見的外部力被稱為變力。從功-能定理的推導角度來看，變力的公式較為複雜。

它可以表示為 $\Delta W = F\left ( x \right ) \Delta x$，其中功的變化依賴於所施加的外力和 x 的變化。

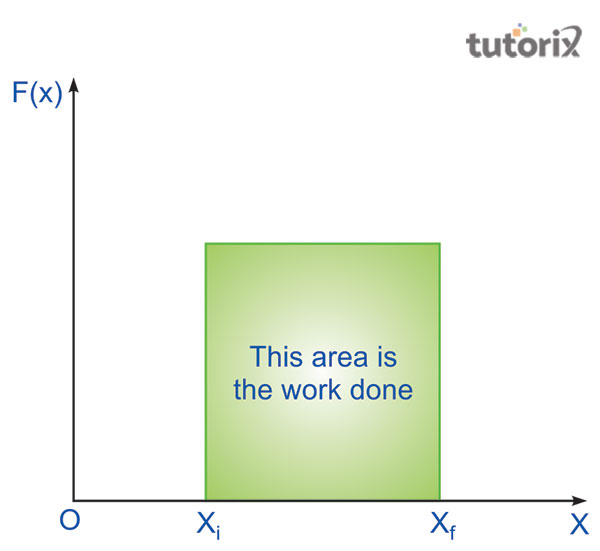
圖 2：變力下的功-能定理

隨著動力的變化，公式描述為 dK/dt = d/dt(1/2 mv²)，根據牛頓第二定律，加速度變為 dK/dt = mav。

由於 F = ma，則速度隨時間的變化率也隨之改變，因此公式變為 dK/dt = F.dx/dt，如果從等式兩邊推匯出時間，則公式表示為 dK = Fdx 或 ΔK = W。

由於該公式證明了功-能定理依賴於變力。

恆力下的功-能定理推導

根據牛頓第二定律，F = ma，其中 m 表示在恆力 F 的作用下運動的物體的質量，a 表示物體的加速度。

對於恆力推導，公式為 Fd = 1/2 m.v₂² – 1/2 m v₁²，其中 F 表示恆力，mv 表示物體的質量速度。在公式中，d 表示物體初始位置和最終位置之間的距離，這裡公式表示 K₂ = m.v₁²/2，表示特定物體的最終動能。

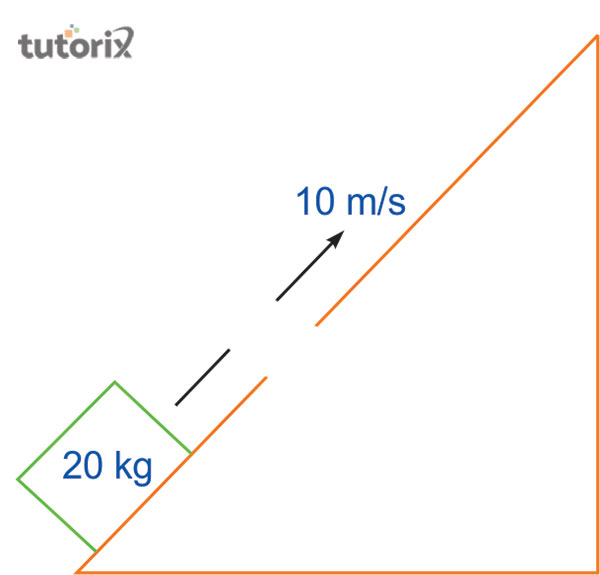
圖 3：恆力下的功-能定理推導

物體的量為 K₁=mv₁²/2，它是特定物體的初始動能。

然後公式變為 W = K₂-K₁=ΔK，其中 ΔK 表示該特定物體的動能變化。

從這個特定的公式可以看出，力對特定物體所做的功等於該物體動能的變化。

功-能定理的特徵及其應用

• 當物體以恆定速度運動時，動能不變，合外力所做的功等於零。

• 功完成後能量才會表現出來，因此能量可以透過物體被其他粒子帶走而減少。

• 它對於理解多個力作用下剛體的運動情況非常有用。

功-能定理的有趣事實

• 它指出外力對物體所做的功等於該特定物體的動能。

• 牛頓第二定律在功-能定理中非常適用。

• 對物體所做的功可以是正的也可以是負的。

結論

功是指外力對物體施加的力，使其從初始位置發生位移。它等於力在位移方向上的分量與位移大小的乘積。功可以用焦耳來衡量，它是它的 SI 單位。所做的功表示從單個物體轉移的總能量，施加外力會影響物體的位移方向。

常見問題

問 1：功-能定理證明了什麼？

答：功-能定理闡明瞭物體動能與對物體所做的功之間的關係。當對物體施加動能導致物體發生位移時，我們就說做了功。

問 2：功-能定理不適用於所有型別的力的原因是什麼？

答：並非所有型別的力都包含非保守因素，因此功-能定理不適用於所有型別的力。功-能定理的公式為 W = KE_f - KE_i = 1/2mv_f² - 1/2mv_i²。

問 3：為什麼功有時是負的？

答：當施加的力與位移方向相反時，功為負。如果力與位移方向相同，則功為正。

問 4：功-能定理的意義是什麼？

答：功-能定理對於測量物體的動能非常有用。它也適用於測量力。