動能和做功

---

簡介

動能是與運動相關的能量。對於靜止的物體，沒有動能。在本文中，我們不討論任何能量變化。例如，水被加熱後轉化為熱能，從而變成蒸汽。我們可以在環境和日常生活中找到許多這樣的能量變化，但它們不在本文的討論範圍之內。在這裡，我們討論與運動物體相關的動能。運動物體由於對其施加的力而獲得動能，這可以用一個公式表示

$\mathrm{KE=\frac{1}{2}mv^2}$

但是功取決於施加在物體上的力和距離。所做的功是施加的力與物體移動距離的乘積。為了獲得所覆蓋的距離，必須做功。對吧？當我們只說“功”時，它是對需要做什麼、需要哪些材料等的範圍定義。但是，當“功”一詞出現在物理學語境中時，可以將其視為“做功”。

什麼是功？

功和做功主要用於相同的含義。然而，在物理學中，我們使用“做功”，因為它等於力和距離的乘積。必須做功才能獲得所覆蓋的距離。對吧？當我們只說“功”時，它是對需要做什麼、需要哪些材料等的範圍定義。但是，當“功”一詞出現在物理學語境中時，可以將其視為“做功”。

什麼是做功？

當對一個物體施加一個力 F 時，它會沿直線或與直線路徑成一定角度移動。如果物體以 $\mathrm{\vartheta}$ 角移動距離 d，則所做的功 W 由以下公式給出

$\mathrm{W=Fd\:Cos(\vartheta)}$

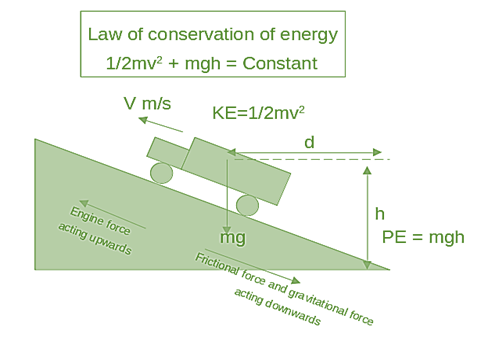
圖 1：物體做的功

正如你在上圖中看到的，發動機正在對輪胎做功以克服摩擦力。同時，輪胎克服道路摩擦力和重力做功。我們知道摩擦力與卡車的運動方向相反。卡車上沒有作用外部力。因此，發動機對輪胎做的有效功抵消了摩擦力和重力，並使卡車以恆定速度 V 向前移動。由於卡車以穩定的速度行駛，因此動能沒有變化 $\mathrm{(\Delta\:V=0)}$。因此，根據功能定理，沒有做功。可以注意到，隨著卡車爬坡，勢能頭 (mgh) 正在增加，從而保持了守恆定律。

做功的型別

定義了三種類型的功。它們是正功、負功和零功。當物體的位移方向與所施加力的方向相同，則為正功。當物體的位移方向與所施加外力的方向相反時，則為負功。當即使對物體施加外力，位移也為零時，則為零功。

示例

什麼時候我們說功是負功？

舉個例子，當你試圖將一輛手推車推上坡時，假設由於手推車中貨物的重量，你正在向下滑動。儘管你向上推著它，但手推車仍在緩慢地向下滾動。這是一種負功的情形。

正功的例子是什麼？一個人爬樹是正功，因為位移方向與人向上施加力的方向相同。

最後，讓我們看一個零功的例子。據說，當一個人拿著一個袋子靜止不動時，所做的功為零。由於重力，袋子的重量向下作用，但由於沒有位移，因此所做的功為零。移動物體是正功。

什麼是動能？

這是物體在運動過程中獲得的能量。與靜止物體相關的能量是勢能。只要有運動，就有動能。例如，放風箏、飛機飛行、鳥類飛行、賽車、旋轉風車、移動的雲、行走、游泳、跑步、軌道衛星、瀑布等等。時鐘的擺動是動能和勢能相互作用的一個例子。當擺錘位於底部中心時，勢能為零，動能最大。在兩端，動能為零，勢能最大 (mgh)。

所有其他能量，如化學能、熱能、機械能、電能等，都是勢能和動能的組合。在任何時間點，這些能量的總和都是一個常數，這就是能量守恆定律。

功能定理

該定理指出，對物體所做的功等於其動能的變化。所做的功以焦耳為單位測量，在公式中表示為

$\mathrm{W=\Delta K=\frac{1}{2}m(v^2-u^2)=m\times a \times d=F \times d}$

已解決示例

序號	本節中使用的函式	公式
1	動能	$\mathrm{KE=\frac{1}{2}mv^2}$
2	做功	$\mathrm{W=Fd}$

• 一輛重 1500 公斤的卡車以 18 公里/小時的速度行駛，試圖用 20000 牛頓的制動力剎車停下。卡車在完全停止前將移動多遠？

$\mathrm{初始動能 =\frac{1}{2}\times 1500 \times (18 \times 60 \times 60/1000)^2=18750\:焦耳}$

最終動能 = 0，因為最終速度為零

動能變化 = 18750 - 0 = 18750 焦耳

制動能量（力）所做的功為 20000 牛頓，這等於動能的變化

$\mathrm{F\times\:d=W=18750}$

$\mathrm{20000\times\:d=18750}$

$\mathrm{d=18750/20000=0.9375 \:米}$

• 一個重 50 公斤的物體以 5 米/秒的速度運動。在運動方向上施加 200 牛頓的力，作用距離為 30 米。物體的最終速度是多少？

$\mathrm{所做的功 =F\:\times\:d = 200\:\times\:30 = 6000\:焦耳}$

應用功能定理，

$\mathrm{6000 = 1/2\:\times\:50\:\times\:{v_f}^2 - 1/2 \:\times\:50\:\times\:5^2 }$

$\mathrm{{v_f}^2=265}$

$\mathrm{最終速度,\:v_f=\sqrt{265}=16.27 米/秒}$

結論

本文全面概述了動能和功的概念，特別是由於功能定理將它們聯絡在一起。對不同型別的功和已解決的示例進行了廣泛的討論。本文闡明瞭功、做功、功率、能量等相關術語之間的區別，以便獲得全面的理解。作為已解決示例部分的序言，列出了所用公式以供參考。常見問題解答和總結提供了其他資訊和要點。

常見問題解答

Q1. 能量和功之間有什麼關係？

A1. 當物體的動能發生變化時，它必須等效於對物體所做的淨功。例如，在直線碰撞中，兩個物體彼此靠近併發生碰撞。所做的總功等於衝擊力乘以衝擊過程中行進的距離。

即平均衝擊力 x 行進距離 = 動能變化。

Q2. 如果一個球被踢出並以恆定速度移動 50 米，則踢球者所做的功是多少？

A2. 由於速度恆定，動能的變化變為零。因此，根據功能定理，所做的功也為零。$\mathrm{\Delta W=\Delta K E}$

Q3. 動能有哪些不同的型別？

A3. 光和聲、電和熱、機械運動。

Q4. 當彈簧從未拉伸狀態拉伸到其長度的兩倍時，它會儲存什麼能量？

A4. 當彈簧被拉伸時，阻力（如彈簧張力）會儲存勢能。

Q5. 力和功的 SI 單位是什麼？

A5. 力以牛頓為單位測量。SI 單位為 $\mathrm{kg\:m\:s^{-2}}$。功以焦耳為單位測量。SI 單位為牛頓米或 $\mathrm{kg \:m^2\:s^{-2}}$。