資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究解釋斯涅爾定律的推導。
斯涅爾定律
斯涅爾定律，也稱為折射定律或斯涅爾-笛卡爾定律。它被定義為“入射角的正弦與折射角的正弦之比對於給定的兩介質對是一個常數”。
公式表示為
$\frac{\sin\ i}{\sin\ r}=\mu =常數\phantom{\rule{0ex}{0ex}}$=折射率
其中，i = 入射角，
r = 折射角， 以及
$(\mu)$ = 常數值，稱為第二介質相對於第一介質的折射率。
因此，它也可以表示為 -
$\frac{Sin{\theta }_{1}}{Sin{\theta }_{2}}=\frac{{n}_{2}}{{n}_{1}}\ 或 \frac{Sin{\theta }_{1}}{Sin{\theta }_{2}}=\frac{{v}_{2}}{{v}_{1}}$
${n}_{1}\ 和\ {n}_{2}=兩個不同介質的折射率$
$\theta_{ 1} =入射角$
$\theta_{ 2} =折射角$
${v}_{1}\ 和\ {v}_{2}=兩個不同介質的相速度$
推導
基本上，斯涅爾定律公式是從費馬原理推匯出來的。
費馬原理指出“光沿最短路徑傳播，並且傳播時間最短”。
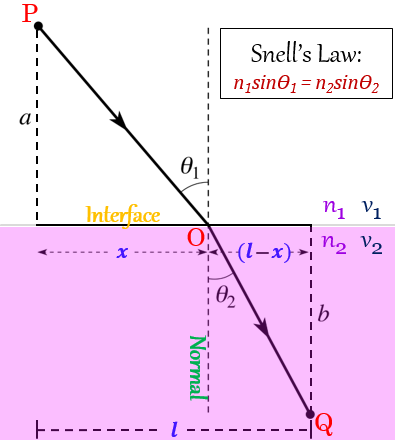
現在我們考慮一條光線從點P傳播到點Q，穿過具有不同折射率的介質，如圖所示。在兩點之間傳播的時間是在每種介質中的距離除以相速度（該介質中光速）。
兩種介質中的相速度表示為 -
${v}_{1}=\frac{c}{{n}_{1}}\ 和\ {v}_{2}=\frac{c}{{n}_{2}}$
這裡，'c' 表示光在真空中的速度。
${v}_{1}\ 和\ {v}_{2}=兩個不同介質的相速度$
${n}_{1}\ 和\ {n}_{2}=兩個不同介質的折射率$
假設 T 是光從 P 透過點 O 到 Q 的傳播時間。
$T=[\frac{(\sqrt[]{{a}^{2}+{x}^{2}})}{{v}_{1}}]+[\frac{(\sqrt[]{{b}^{2}+(l-x{)}^{2}})}{{v}_{2}}]$
$T=[\frac{(\sqrt[]{{a}^{2}+{x}^{2}})}{{v}_{1}}]+[\frac{(\sqrt[]{{b}^{2}+{l}^{2}-2lx+{x}^{2}})}{{v}_{2}}]$
其中 $a$、$b$、$l$ 和 $x$ 如下圖所示，$x$ 是變化引數。
為了使時間最小化，我們將時間相對於 $x$ 的導數設定為
零。我們還使用正弦的定義（對邊/斜邊）來
將長度與入射角和反射角相關聯。
$\frac{dT}{dx}=\frac{x}{{v}_{1}\sqrt{{x}^{2}+{a}^{2}}}+\frac{-(l-x)}{{v}_{2}\sqrt{(l-x{)}^{2}+{b}^{2}}}=0$（駐點）
注意，$\frac{x}{\sqrt{{x}^{2}+{a}^{2}}}=sin{\theta }_{1}$ 和 $\frac{x}{\sqrt{(l-x{)}^{2}+{b}^{2}}}=sin{\theta }_{2}$
$\frac{dT}{dx}=\frac{\sin{\theta }_{1}}{{v}_{1}}-\frac{\sin{\theta }_{2}}{{v}_{2}}=0$
$\frac{\sin{\theta }_{1}}{{v}_{1}}=\frac{\sin{\theta }_{2}}{{v}_{2}}$
透過代入相速度方程，我們得到 -
$\frac{{n}_{1}\sin{\theta }_{1}}{c}=\frac{{n}_{2}\sin{\theta }_{2}}{c}$ [$\because{v}_{1}=\frac{c}{{n}_{1}}\ 和\ {v}_{2}=\frac{c}{{n}_{2}}$]
${n}_{1}\sin{\theta }_{1}={n}_{2}\sin{\theta }_{2}$ .............. 這是最終推匯出的斯涅爾定律方程。
注意：- 使用微積分來推導斯涅爾定律。（不在 10 年級課程大綱中）
3K+ 次瀏覽
