圓的弦、弦長及其定理

---

引言

弦是連線圓周上任意兩點的線段。圓是歐幾里得幾何中眾所周知的二維圖形。它具有各種組成部分，包括弦、半徑、直徑等。在本教程中，我們將討論圓的弦的定義、公式和一些相關定理。

圓

• 圓是在平面上繪製的二維圖形，圓上每一點到一個固定點的距離相等。

• 該固定點稱為圓心。

• 圓的尺寸用其半徑表示。

• 圓心與圓上任意一點之間的距離稱為半徑。

• “圓”這個詞來源於拉丁語“circulus”（意為小環）。圓的圖形表示如下所示。

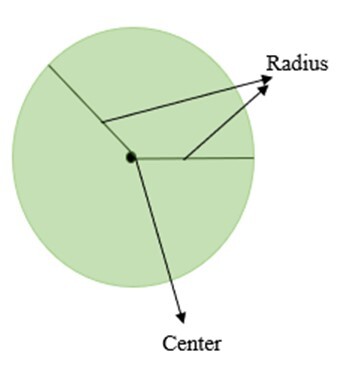
圓具有多種性質，下面簡要總結。

• 圓是一個曲面，任何直線都界定了曲面區域。因此，它不屬於多邊形類別。

• 具有相同半徑的圓被認為是全等圓。

• 任何弦的垂直平分線都經過圓心。

• 最長的弦是圓的直徑。

• 連線兩個圓的交點的線段垂直於連線這兩個圓的圓心的線段。

• 圓可以內接於三角形或正方形。

• 在直徑的端點處畫出的切線彼此平行。

圓的弦

• 弦是連線圓上任意兩點的線段。

• 換句話說，弦的端點位於圓周上。

• 在圓中可以畫出無限多條弦。

• 線段AB、CD和EF是下圖中表示的一些弦。

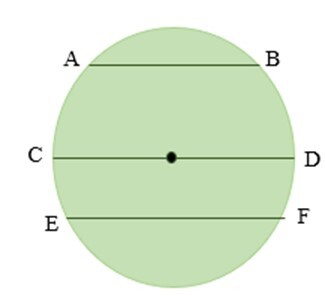
弦有以下幾種性質。

• 直徑是圓中最長的弦。

• 弦將圓分成兩部分。

• 直徑將圓分成兩等分。

• 當弦在兩側延伸時，它被稱為割線。

已知弦到圓心的距離求弦長

如果已知弦到圓心的距離，則可以使用以下公式計算弦長。

$$\mathrm{S\:=\:2\sqrt{(r^{2}\:-\:p^{2})}}$$

其中 r = 圓的半徑

p = 弦到圓心的垂直距離

S = 弦長

證明 −

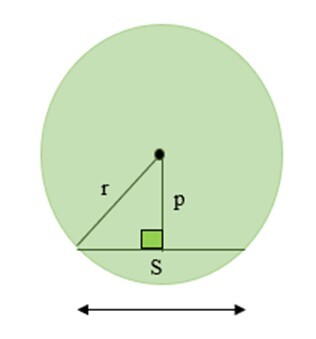
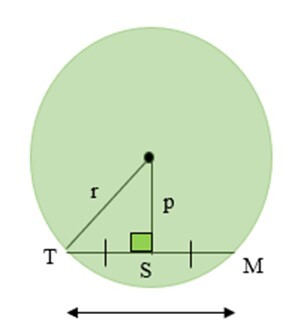
在上圖中，直角三角形的斜邊是圓的半徑。垂直平分線是三角形的一條邊。眾所周知，垂直線平分弦。因此，弦長將是直角三角形底邊的兩倍。

現在，使用勾股定理，

$$\mathrm{底邊\:=\:\sqrt{(r^{2}\:-\:p^{2})}}$$

$$\mathrm{\Longrightarrow\:弦長\:=\:2\times\:底邊\:=\:2\sqrt{(r^{2}\:-\:p^{2})}}$$

已知圓心角求弦長

讓我們考慮一個半徑為r、弦長為S的圓。弦在圓心處成θ角。

使用三角函式，弦長 $\mathrm{=\:2\times\:r\times\:\sin\frac{\theta}{2}}$

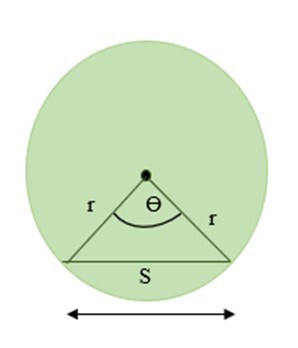
圓的弦定理

與弦相關的各種定理如下所述。

• 定理 1 − 從圓心到弦所作的垂線平分弦。在給定圖中，TS = SM。

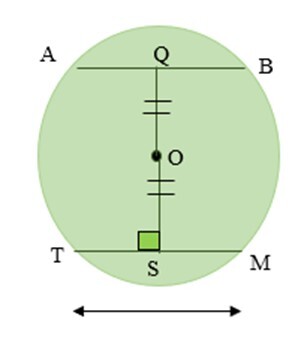
• 定理 2 − 如果從圓心到各自弦的垂線長度相等，則兩條弦相等。在給定圖中，TM = AB。

• 定理 3 − 如果兩條弦在圓心處張成的角相等，則兩條弦相等。

• 定理 4 − 對於兩條不相等的弦，較長的一條比較短的一條更靠近圓心。

例題

1) 在給定圖中，OP = 10 釐米，TS = 6 釐米。求弦 TM 的長度？

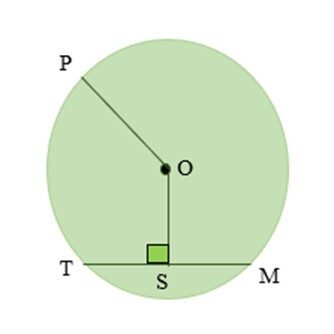
答案 −

圓的半徑 $\mathrm{=\:r\:=\:OP\:=\:10\:釐米}$

直角三角形的底邊 = TS = 6 釐米

使用勾股定理，

$$\mathrm{OS\:=\:\sqrt{(OP^{2}\:-\:TS^{2})}}$$

$$\mathrm{\Longrightarrow\:OS\:=\:\sqrt{(10^{2}\:-\:6^{2})}}$$

$$\mathrm{\Longrightarrow\:OS\:=\:\sqrt{64}\:=\:8\:釐米}$$

使用弦的公式，

$$\mathrm{\Longrightarrow\:弦長\:=\:2\sqrt{(半徑^{2}\:-\:垂線^{2})}}$$

$$\mathrm{\Longrightarrow\:弦長\:=\:2\sqrt{(10^{2}\:-\:8^{2})}}$$

$$\mathrm{\Longrightarrow\:弦長\:=\:12\:釐米}$$

∴ 弦長為 12 釐米。

2) 如果 OT = 15 釐米且 OS = 4 釐米，求弦長和 TS。

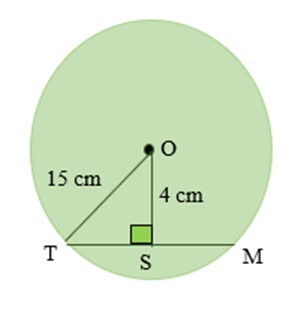
答案 −

在直角三角形 OTS 中，

$$\mathrm{OT^{2}\:=\:OS^{2}\:+\:TS^{2}}$$

$$\mathrm{\Longrightarrow\:15^{2}\:=\:4^{2}\:+\:TS^{2}}$$

$$\mathrm{\Longrightarrow\:TS^{2}\:=\:15^{2}\:-\:4^{2}}$$

$$\mathrm{\Longrightarrow\:TS^{2}\:=\:225\:-\:16\:=\:209}$$

$$\mathrm{\Longrightarrow\:TS\:=\:\sqrt{209}\:=\:14.46\:釐米}$$

弦長 $\mathrm{=\:TM\:=\:2\times\:TS\:=\:2\times\:14.46\:=\:28.92\:釐米}$

∴ 弦長和 TS 分別為 28.92 釐米和 14.46 釐米。

文字題

• 問題 1 − 如果直徑長和從圓心到弦的垂線長分別為 18 釐米和 3 釐米，求弦長。

• 問題 2 − 一條弦在圓心處張成 30° 的角。圓的半徑為 10 釐米。求弦長。

• 問題 3 − 圓的弦是半徑的一半。求弦在圓心處張成的角。

結論

本教程簡要介紹了弦及其各種性質。此外，還簡要介紹了與弦長相關的基本公式。本教程中說明了與圓的弦相關的某些定理。此外，還提供了一些例題，以更好地理解這個概念。總之，本教程可能有助於理解弦及其定理的基本概念。

常見問題

1. 弦的長度可以小於圓的半徑嗎？

是的。弦的長度並不一定總是大於半徑。

2. 在圓中可以畫多少條弦？

在圓中可以畫出無限多條弦。然而，直徑是圓中最長的弦。

3. 弦和扇形有什麼區別？

弦是連線圓周上任意兩點的線段，而扇形是圓的一部分，由兩條半徑和一條弧組成。一個圓可以分成兩個扇形，而一個圓中可以畫出無限多條弦。

4. 切線可以稱為弦嗎？

切線是隻與圓相交於一點的線段，而弦是與圓相交於兩點的線段。因此，切線不能稱為弦。

5. 當兩條半徑連線弦的兩端時，會形成什麼樣的三角形？

如果兩條半徑連線弦的端點，則會形成等腰三角形。此外，從圓心到弦的垂線平分弦。