布儒斯特角定律：定義、公式、示例

---

介紹

布儒斯特角定律是光學（光的科學）中研究的內容。如果光波能夠完美地穿過所有材料，你將什麼也看不到，所有材料都會變得隱形。另一方面，如果材料完美地反射所有光線，它們將始終呈現白色而不是彩色。顏色之所以可見，是因為材料吸收特定波長並反射其他波長。實際上，所有材料都選擇性地反射、透射或吸收光線。

同時，具有特定特性的光波可以完全透射透過特定表面。這涉及到特定**偏振**的光以一定角度入射到表面上，然後被完全透射。首先，讓我們瞭解什麼是偏振。

如果你還記得，**光**是一種**電磁**波，因此包含電場和磁場。光線的電場分量振動的方向決定了它的偏振方向，簡而言之，就是它的偏振。

什麼是布儒斯特角定律？

當光入射到透明表面的邊界時，反射和透射的光量取決於介質的**折射率**和入射波的偏振。布儒斯特角定律是一種關係式，它為我們提供了發生完全透射時的入射角。

示例：一塊玻璃的**折射率**為1.5，如果放在空氣中，**布儒斯特角**大約為56°。有趣的是，由於布儒斯特角取決於兩種介質的折射率，因此空氣到玻璃的布儒斯特角值將不同於水到玻璃的布儒斯特角值。

另一個需要注意的重要點是，當非偏振光以布儒斯特角入射時，反射分量在一個特定方向上是**完全偏振的**，而折射光線是部分偏振的。這使得我們可以透過反射產生特定方向偏振的光波。

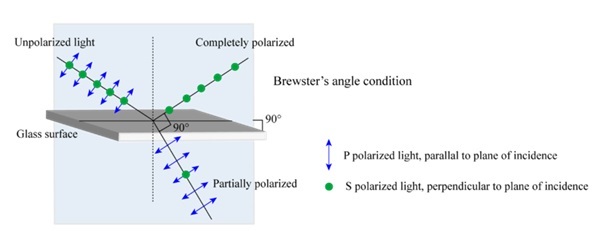
Sobarwiki，布儒斯特角偏振，標記為公共領域，Wikimedia Commons 上有更多詳細資訊

布儒斯特角定律公式

如果我們分別用 $\mathrm{n_1}$ 和 $\mathrm{n_2}$ 表示第一種和第二種介質的**折射率**，則布儒斯特角由下式給出：

$$\mathrm{\theta_B=\arctan{\frac{n_2}{n_1}}}$$

回顧一下柯西關係。材料的折射率不是一個普遍常數，它本身是波長的函式。因此，不同波長的光的布儒斯特角是不同的。但是，對於可見光區域，布儒斯特角的變化很小。

布儒斯特角推導

可以使用斯涅耳定律得到布儒斯特角的一個簡潔而簡單的推導。

當來自折射率為 $\mathrm{n_1}$ 的材料的光以 $\mathrm{\theta_1}$ 角入射到折射率為 $\mathrm{n_2}$ 的材料上時，折射角 $\mathrm{\theta_2}$ 與這些量之間的關係為：

$$\mathrm{n_1\:sin\:\theta_1 =n_2\:sin \: \theta_2}$$

現在，事實證明，光波與介質的物理相互作用方式是，當 $\mathrm{\theta_2=90^{\circ}-\theta_1}$ 時，反射為零。因此，

$$\mathrm{n_1\:sin\:\theta_1 =n_2\:sin \: (90^{\circ}-\theta_1)}$$

$$\mathrm{\frac{sin\:\theta_1}{cos\: \theta_1}=\frac{n_2}{n_1}}$$

現在，正弦除以餘弦就是正切。這裡的 $\mathrm{θ_1}$ 就是布儒斯特角 $\mathrm{θ_B}$。因此，

$$\mathrm{tan\:\theta_B=\frac{n_2}{n_1}}$$

或者，

$$\mathrm{\theta_B=\arctan{\frac{n_2}{n_1}}}$$

可以使用麥克斯韋方程組、相關的邊界條件和菲涅耳公式得到該關係式的更全面的證明。

布儒斯特角和臨界角之間的關係

你一定還遇到過臨界角的概念。兩種介質介面的臨界角定義為折射光線與法線成 $\mathrm{90^{\circ}}$ 角時的角度。也就是說，超過臨界角，所有光線都會被反射，不會發生折射。這被稱為全內反射。

臨界角可以透過簡單地應用斯涅耳定律來找到。如果 $\mathrm{\theta_C}$ 是臨界角，則

$$\mathrm{n_1\:sin\:\theta_C =n_2\:sin\: 90^{\circ}=n_2}$$

因此，

$$\mathrm{sin\:\theta_C=\frac{n_2}{n_1}}$$

我們可以將右邊的分數等同於布儒斯特角的正切。因此，

$$\mathrm{sin\:\theta_C=tan\:\theta_B}$$

這就是布儒斯特角和臨界角之間的關係。

布儒斯特角定律的應用

布儒斯特角定律在各種情況下都有應用：

• 你一定聽說過**偏光太陽鏡**。這些太陽鏡塗有特定折射率的薄膜，可以透過反射阻擋從表面反射的光線，從而減少眩光。

• 攝影師會在鏡頭前放置**偏振濾光鏡**，減少來自水平表面（如水面）的眩光，並允許他們拍攝反射表面下的物體。例如，如果你看到過清晰地顯示湖中魚類和動植物的湖泊影像，它很可能就是透過偏振鏡頭拍攝的。

• 只能從一面看到而另一面反射的窗戶是基於偏振的概念。

• **全息圖**是由光波的干涉記錄的。如果發生不需要的反射，則會出現噪聲。相反，用於記錄全息圖的雷射束是偏振的，並且以布儒斯特角入射。這使得產生的全息圖更清晰。

• 在研究不同材料的**光學特性**時，以布儒斯特角入射的光線將被完美透射，從而減少不需要的反射損耗。

結論

我們知道，沒有哪種材料是光的完美反射體、吸收體或透射體。如果存在這樣的材料，它們將是隱形的、完全白色的或黑色的。相反，光的部分總是被反射或吸收。特定偏振的光可以被完全透射。請注意，**光的偏振**是指其電場分量振動的方向。當特定方向偏振的光以一定角度入射到透明介面的邊界時，不會吸收反射。這個角度稱為布儒斯特角，這個角度和所涉及的兩種材料的折射率之間的關係由布儒斯特角定律給出，其公式為

$$\mathrm{\theta_B=\arctan{\frac{n_2}{n_1}}}$$

由於折射率取決於波長，因此布儒斯特角對於入射到同一介面的不同波長的光線是不同的。此外，布儒斯特角可以與臨界角聯絡起來，臨界角是發生全內反射時的角度。

$$\mathrm{sin\:\theta_C =tan\:\theta_B}$$

布儒斯特角定律在許多情況下都有應用。偏光太陽鏡、偏振濾光鏡、單向透視窗和全息圖記錄只是一些布儒斯特角定律發揮作用的例子。

常見問題

Q1. 折射率是如何與波長相關的？

A1. 柯西方程給出了折射率與波長的關係。

$$\mathrm{n=A+\frac{B}{\lambda^2}+\frac{C}{\lambda^4}+.....}$$

這裡，A、B 和 C 是常數，而 λ 是光的波長。

Q2. 當非偏振光以布儒斯特角入射到介面上時，哪個偏振方向會被反射？

A2. 垂直於入射面的偏振光波將被反射。這也被稱為 s 偏振。

Q3. 非偏振光是什麼意思？

A3. 非偏振光是由所有可能方向偏振的光波組成的。因此，沒有偏振相當於 $\mathrm{360^{\circ}}$ 偏振。

Q4. 我們如何獲得偏振光？

A4. 各種材料只允許特定偏振的光線透過。如果我們想獲得特定方向偏振的光線，我們應該將這些材料放置在光束的路徑上。還有許多其他方法可以獲得偏振光。我們可以透過反射、散射甚至折射產生偏振光。

Q5. 偏振會影響光波的強度嗎？

A5. 會影響。透過偏振器的光強度與入射光束 θ 的強度有關。當非偏振光透過偏振器時，其強度減半。