相似三角形的面積

---

介紹

相似三角形的面積定理有助於建立兩個相似三角形面積之間的關係。形狀和大小相同的幾何圖形稱為全等圖形。

例如：半徑相同的任意兩個圓是全等的。

長度和寬度相同的任意兩個矩形是全等的。

但是，形狀相同但大小不同的幾何圖形稱為相似圖形。全等圖形總是相似的，但兩個相似圖形不一定是全等的。

例如：任意兩個圓是相似的。任意兩個矩形是相似的。

三角形的相似用符號“~”表示。

相似三角形

• 如果兩個三角形的角相等（對應角），並且它們的邊成比例（對應邊），則這兩個三角形是相似的。

• 相似三角形可能具有不同的邊長，但它們的角必須相等，並且對應邊的比例必須相等。

• 如果兩個三角形相似，則意味著對應三角形的角對都相等。三角形的所有對應邊都成比例。

• 用符號“~”表示相似。

• 因此，如果兩個三角形相似，則表示為△QPR ~ △XYZ。

相似三角形區域集

• 相似三角形區域集有助於建立兩個相似三角形區域之間的關係。

• 它指出：“兩個相似三角形的面積之比等於任何一對對應邊之比的平方”。

• 讓我們看下圖，它顯示了兩個相似三角形ΔABC和ΔDEF。

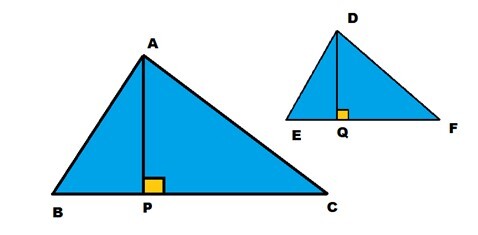
相似三角形的面積

根據相似三角形定理，

$$\mathrm{ΔABC面積/ΔDEF面積 = \frac{(AB)^2}{(DE)^2} =\frac{(BC)^2}{(EF)^2} =\frac{(AC)^2}{(DF)^2}}$$

相似三角形面積之比

結論 - 兩個相似三角形的面積之比等於每一對對應邊之比的平方。

已知 - 考慮兩個三角形ΔABC和ΔDEF，使得ΔABC~ΔDEF

證明 - $\mathrm{ΔABC面積/ΔDEF面積 = \frac{(AB)^2}{(DE)^2} =\frac{(BC)^2}{(EF)^2} =\frac{(AC)^2}{(DF)^2}}$

作圖：分別在邊BC和EF上作高AP和DQ，如上圖所示。

[ ∵ ΔABC ~ ΔDEF ] 且

$$\mathrm{\angle APB =\angle DQE.}$$

[ ∵ AP和DQ分別垂直於邊BC和EF ⇒每個角都等於90°]

根據三角形的相似性，我們說ΔABP和ΔDEQ是等角的。

所以ΔABP ~ ΔDEQ

所以 $\mathrm{\frac{AP}{DQ} =\frac{AB}{DE}}$

此外

$$\mathrm{\frac{AP}{DQ} = \frac{BC}{EF}----- (1)...[∵ ΔABC\sim ΔDEF \Rightarrow \frac{AB}{DE} = \frac{BC}{EF}]}$$

所以

Area(ΔABC)/Area(ΔDEF) $\mathrm{=\frac{[(\frac{1}{2}) × BC × AP]}{[(\frac{1}{2}) × EF × DQ]}}$

$$\mathrm{= (\frac{BC}{EF}) × (\frac{AP}{DQ})= (\frac{BC}{EF}) × (\frac{BC}{EF})....[From (1)]}$$

⇒ Area(ΔABC)/Area(ΔDEF) = $\mathrm{(\frac{BC}{EF})^2}$

同樣地，

ΔABC面積/ΔDEF面積 =$\mathrm{=\frac{(AB)^2}{(DE)^2}=\frac{(BC)^2}{(EF)^2}=\frac{(AC)^2}{( DF)^2}}$

例題

1)有兩個相似三角形，ΔABC，ΔDEF。它們的邊之比分別為2:5。如果Ar(ΔABC)為28，則Ar(ΔDEF)是多少？

答案：我們知道，

ΔABC面積/ΔDEF面積 =$\mathrm{=\frac{(AB)^2}{(DE)^2}=\frac{(BC)^2}{(EF)^2}=\frac{(AC)^2}{( DF)^2}}$

因此，$\mathrm{\frac{28}{Ar(ΔDEF)} = (\frac{AB}{DE})^2 = (\frac{2}{5})^2}$,

$$\mathrm{\Rightarrow \frac{28}{Ar(ΔDEF)} = \frac{4}{25}}$$

$$\mathrm{\Rightarrow Ar(ΔDEF) = 28×\frac{25}{4}=7×25=175\: 平方單位}$$

2)有兩個相似三角形，ΔABC，ΔDEF。它們的邊之比分別為2:3。如果Ar(ΔABC)為12，則Ar(ΔXYZ)是多少？

答案：我們知道，

ΔABC面積/ΔXYZ面積 =$\mathrm{=\frac{(AB)^2}{(XY)^2}=\frac{(BC)^2}{(YZ)^2}=\frac{(AC)^2}{(XZ)^2}}$

$$\mathrm{因此， \frac{12}{Ar(ΔXYZ)} = (\frac{AB}{XY})^2 = (\frac{2}{3})^2,}$$

$$\mathrm{\Rightarrow \frac{12}{Ar(ΔDEF)} = \frac{4}{9}}$$

$$\mathrm{\Rightarrow Ar(ΔXYZ) = 12×\frac{9}{4}=3×9=27\: 平方單位}$$

3)有兩個相似三角形，ΔABC，ΔDEF。它們的面積分別為20, 50。如果AC為2，則DF是多少？

答案：我們知道，

ΔABC面積/ΔDEF面積 =$\mathrm{=\frac{(AB)^2}{(DE)^2}=\frac{(BC)^2}{(EF)^2}=\frac{(AC)^2}{( DF)^2}}$

$$\mathrm{因此，\frac{20}{50}=\frac{2}{DF}; DF=5}$$

所以，DF的長度是5個單位。

4)有兩個相似三角形，ΔABC，ΔXYZ。它們的面積分別為30, 40。如果AC為3，則XZ是多少？

答案：我們知道，

ΔABC面積/ΔXYZ面積 =$\mathrm{=\frac{(AB)^2}{(XY)^2}=\frac{(BC)^2}{(YZ)^2}=\frac{(AC)^2}{(XZ)^2}}$

$$\mathrm{因此， \frac{30}{40}=\frac{3}{XZ}; XZ=4}$$

所以，XZ的長度是4個單位。

5)有兩個相似三角形，ΔABC，ΔDEF。它們的邊之比分別為1:2。如果Ar(ΔPQR)為10，則Ar(ΔXYZ)是多少？

答案：我們知道，

$$\mathrm{ΔPQR面積/ΔXYZ面積 = \frac{(PQ)^2}{(XY)^2}=\frac{(QR)^2}{(YZ)^2}=\frac{(PR)^2}{(XZ)^2}}$$

$$\mathrm{因此， \: \frac{10}{Ar(ΔXYZ)} = (\frac{PQ}{XY})^2 = (\frac{1}{2})^2,}$$

$$\mathrm{\Rightarrow \frac{10}{Ar(ΔDEF)} =\frac{1}{4}}$$

$$\mathrm{\Rightarrow Ar(ΔXYZ) = 10×\frac{4}{1}=10×4=40\: 平方單位}$$

6)有兩個相似三角形，ΔABC，ΔDEF。它們的面積分別為100, 600。如果AC為10，則DF是多少？

答案：我們知道，

ΔABC面積/ΔDEF面積 =$\mathrm{=\frac{(AB)^2}{(DE)^2}=\frac{(BC)^2}{(EF)^2}=\frac{(AC)^2}{( DF)^2}}$

因此， $\mathrm{\frac{100}{600}=\frac{10}{DF}}$; DF=60

所以，DF的長度是60個單位。

7)有兩個相似三角形，ΔPQR，ΔXYZ。它們的面積分別為80, 90。如果PR為8，則XZ是多少？

答案：我們知道，

$$\mathrm{ΔPQR面積/ΔXYZ面積 = \frac{(PQ)^2}{(XY)^2}=\frac{(QR)^2}{(YZ)^2}=\frac{(PR)^2}{(XZ)^2}}$$

因此， $\mathrm{\frac{80}{90}=\frac{8}{XZ}}$; XZ=9

所以，XZ的長度是9個單位。

8)有兩個相似三角形，ΔPQR，ΔDEF。它們的面積分別為30, 50。如果PR為3，則DF是多少？

答案：我們知道，

$$\mathrm{ΔPQR面積/ΔDEF面積 = \frac{(PQ)^2}{(DE)^2}=\frac{(QR)^2}{(EF)^2}=\frac{(PR)^2}{(DF)^2}}$$

因此， $\mathrm{\frac{30}{50}=\frac{3}{DF}}$; DF=5

所以，DF的長度是5個單位。

結論

在本教程中，我們學習了相似三角形以及將兩個相似三角形的面積比與它們對應邊的比聯絡起來的定理。兩個相似三角形的面積之比等於任何一對對應邊之比的平方。對於相似三角形ΔABC和ΔDEF，ΔABC面積/ΔDEF面積 $\mathrm{=\frac{(AB)^2}{(DE)^2}=\frac{(BC)^2}{(EF)^2}=\frac{(AC)^2}{( DF)^2}}$ 相似三角形的相關角都相等，所有對應邊都成比例。

常見問題

1. 用你自己的話簡要解釋一下什麼是相似三角形。

形狀相同但大小不同的幾何圖形稱為相似圖形。全等圖形總是相似的，但兩個相似圖形不一定是全等的。例如，任意兩個圓是相似的，但如果它們的半徑不同，則它們不全等。

2. 簡要解釋一下相似三角形的符號是什麼。

假設有兩個三角形XYZ和GHI。然後我們可以用∆XYZ ~ ∆GHI來表示它們。

3. 我們能否認為相似三角形和全等三角形幾乎相同？

全等圖形總是相似的，但兩個相似圖形不一定是全等的。例如，任意兩個圓是相似的，但如果它們的半徑不同，則它們不全等。

4. 在相似三角形的情況下，可以應用哪些三個定理來證明它們是相似的？

在相似三角形的情況下，可以應用以下三個定理來證明它們是相似的：

• 角角 (AA)

• 邊角邊 (SAS)

• 邊邊邊 (SSS)

5. 我們如何理解相似三角形的邊之間的比例關係？

如果相似三角形的邊分別為P、Q、R和p、q、r，則它們之間的比例關係為：

P : p = Q : q = R : r。