基本比例定理與相似三角形

---

引言

基本比例定理是由著名的希臘數學家泰勒斯提出的，因此也稱為泰勒斯定理。三角形是具有三條邊和三個角的基本幾何形狀之一。在幾何學中，你已經學習了三角形的不同性質和定理。在本教程中，我們將學習最重要的性質之一，即相似性和基本比例定理。如果兩個三角形的角全等且對應邊成比例，則稱這兩個三角形相似。“$\mathrm{\sim}$”符號用於表示相似三角形。判斷三角形是否相似的方法有很多，它基於三角形相似性的性質。

三角形的相似性

如果兩個幾何圖形具有相同的形狀，但不一定具有相同的大小，則稱它們相似。當相似圖形放大或縮小時，可以互相重疊。當它們以不同的方向放置時，它們可以互相重疊。

如果兩個三角形的角相等且對應邊成比例，則稱這兩個三角形相似。“$\mathrm{\sim}$”符號用於表示相似三角形。

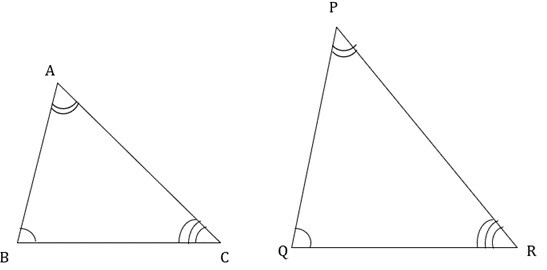
在上圖中：

如果 $\mathrm{\angle A \cong \angle P}$

$\mathrm{\angle B \cong \angle Q}$

$\mathrm{\angle C \cong \angle R}$

並且 $\mathrm{\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR}}$

從上面可以看出，兩個三角形的角相等，且邊成比例。

因此，△ABC和△PQR是相似三角形。

數學上可以表示為：△ABC ∼ △PQR。

相似三角形的一些性質

自反性

每個三角形都與自身相似。例如，△ABC ∼ △ABC

對稱性

如果△ABC ∼ △PQR，則△PQR ∼ △ABC

傳遞性

如果△ABC ∼ △PQR且△PQR ∼ △XYZ，則△ABC ∼ △XYZ

相似判別準則

• 利用相似判別準則，我們可以證明三角形是否相似。

• 檢驗三角形相似性有三個準則，如下所示：

  • AAA 準則

  • SSS 準則

  • SAS 準則

AAA 準則

• 如果兩個三角形的對應角相等，則它們的對應邊成比例。

• 這個準則被稱為兩個相似三角形的AAA（角角角）準則。

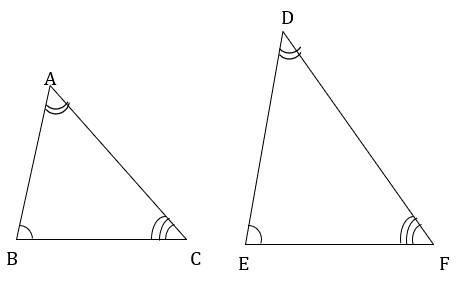
在△ABC和△DEF中，對應關係為ABC ↔ PQR

$$\mathrm{\angle A \cong \angle D}$$

$$\mathrm{\angle B \cong \angle E}$$

$$\mathrm{\angle C \cong \angle F}$$

給定的三角形滿足AAA準則。

因此，△ABC ∼ △DEF。

如果一個三角形的兩個角與另一個三角形的兩個對應角全等，則這兩個三角形相似。這被稱為兩個三角形相似的AA準則。

SSS 準則

• 在兩個三角形中，如果一個三角形的邊與另一個三角形的邊成比例，則它們的對應角相等，這兩個三角形相似。

• 這被稱為相似三角形的SSS（邊邊邊）準則。

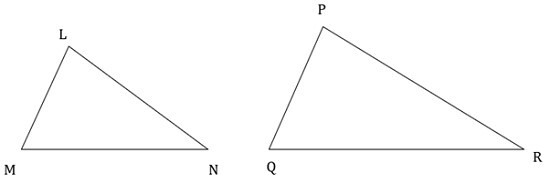
在△LMN和△PQR中

$$\mathrm{\frac{LM}{PQ}=\frac{MN}{QR}=\frac{LN}{PR}}$$

給定的三角形滿足SSS準則

因此，△LMN ∼ △PQR

SAS 準則

• 在兩個三角形中，如果一個三角形的一個角等於另一個三角形的一個角，並且包含該角的邊成比例，則這兩個三角形相似。

• 這被稱為相似三角形的SAS（邊角邊）準則。

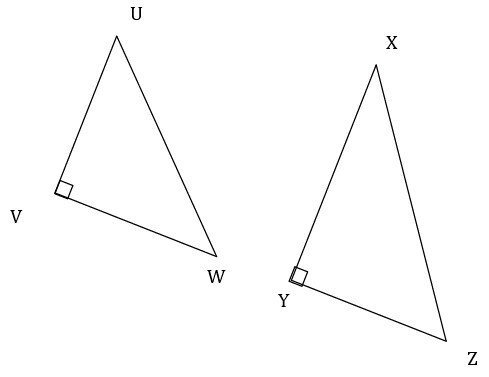
在△UVW和△XYZ中

如果 $\mathrm{\angle V \cong \angle Y}$

並且 $\mathrm{\frac{UV}{XY}=\frac{VW}{YZ}}$

因此，上述三角形滿足SAS準則，

因此△UVW ∼ △XYZ

如果已知每個三角形的一條邊和一個角，則可以使用此準則。

基本比例定理 (BPT)

定理：如果一條平行於三角形一邊的直線與其餘兩邊相交於兩個不同的點，則這條直線將其餘兩邊按比例分割。

證明

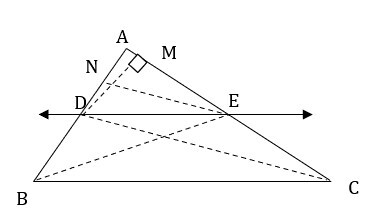
已知：在△ABC中，直線DE∥直線BC

直線DE分別與直線AB和AC相交於點D和E。

證明：$\mathrm{\frac{AD}{DB}=\frac{AE}{EC}}$

作圖：連線BE和CD，然後作DM⊥AC和EN⊥AB

證明：△ADE的面積 = $\mathrm{\frac{1}{2}×AD×EN}$

同樣，△BDE的面積 = $\mathrm{\frac{1}{2}×DB×EN}$

△ADE的面積 = $\mathrm{\frac{1}{2}×AE×DM}$ 和 △BDE的面積 = $\mathrm{\frac{1}{2}×EC×DM}$

△ADE和△BDE有相同的高EN

因此，$\mathrm{\frac{△ADE的面積}{△BDE的面積}=\frac{AD}{DB} …………..(i)}$

同樣，△ADE和△DEC有相同的高DM

因此，$\mathrm{\frac{△ADE的面積}{△DEC的面積}=\frac{AE}{EC} …………..(ii)}$

△BDE和△DEC有相同的底邊DE，且直線BC∥直線DE。

因此，△BDE的面積 = △DEC的面積……(iii)

因此，由(i)、(ii)和(iii)可得：

$$\mathrm{\frac{AD}{DB}=\frac{AE}{EC}}$$

例題

1) 檢查下列三角形是否相似？如果是，請解釋使用哪種檢驗方法？

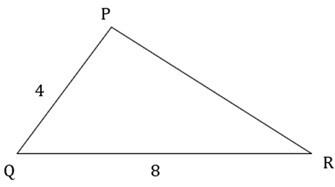
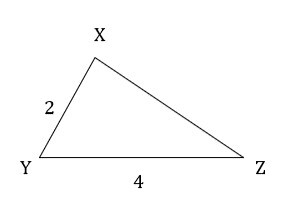
答：在△PQR和△XYZ中

$$\mathrm{\frac{PQ}{XY}=\frac{4}{2}=2 \: \& \: \frac{QR}{YZ}=\frac{8}{4}=2}$$

因此，$\mathrm{\frac{PQ}{XY}=\frac{QR}{YZ}}$

並且 $\mathrm{\angle M \cong \angle Y}$ ……(已知)

△PQR ∼ △XYZ ……(相似性的SAS準則)

2) 在給定圖形中，AB∥EF，則證明△AOB ∼ △EOF。

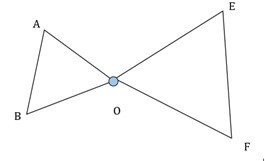
答：AB∥EF ……(已知)

$\mathrm{\angle A =\angle F}$ ……(內錯角)

$$\mathrm{\angle B =\angle F}$$

$\mathrm{\angle AOB =\angle EOF}$ ……(對頂角)

因此△AOB ∼ △EOF。

3) 1) 在△PQR中，直線AB∥QR

如果QA = 4.8釐米，PA = 1.6釐米，BR = 6.4釐米，則求PB。

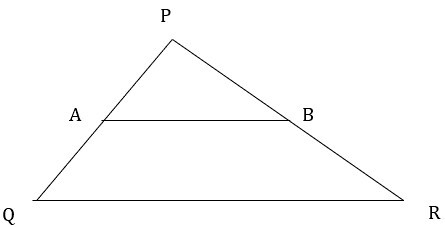
答：在△PQR中，AB∥QR ……(已知)

根據基本比例定理，

$$\mathrm{\frac{PA}{AQ}=\frac{PB}{BR}}$$

$$\mathrm{\frac{1.6}{4.8}=\frac{PB}{6.4}}$$

$$\mathrm{PB=\frac{1.6\times 6.4}{4.8}}$$

$$\mathrm{PB = 2.1 釐米}$$

結論

三角形的相似性是三角形的重要性質之一。

如果兩個三角形的角全等且對應邊成比例，則稱這兩個三角形相似。基本比例定理是由希臘數學家泰勒斯提出的。它指出，如果一條直線平行於三角形的一邊，則它與另外兩邊相交於兩個不同的點，並將這兩邊按相同的比例分割。

常見問題

1. 什麼是全等三角形？

如果任何兩個三角形的兩個對應角和邊相等，則這兩個三角形被稱為全等三角形。

2. 指出總是相似的三角形的型別。

等邊三角形和兩個等腰直角三角形總是相似的。

3. 說明相似三角形面積定理。

它指出，當兩個三角形相似時，這兩個三角形的面積之比等於它們對應邊平方之比。

4. 基本比例定理是否適用於斜三角形？

是的。基本比例定理適用於所有三角形。

5. 基本比例定理有哪些應用？

基本比例定理用於證明以下性質：

• 三角形角平分線的性質。

• 三條平行線及其截線的性質。