資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究從以下四個選項中選擇正確的答案
在三角形\( \mathrm{ABC} \)和\( \mathrm{DEF} \)中，\( \angle \mathrm{B}=\angle \mathrm{E} \)，\( \angle \mathrm{F}=\angle \mathrm{C} \)且\( \mathrm{AB}=3 \mathrm{DE} \)。
(A) 全等但不同相似
(B) 相似但不同等
(C) 既不同等也不相似
(D) 既全等又相似
已知
在三角形\( \mathrm{ABC} \)和\( \mathrm{DEF} \)中，\( \angle \mathrm{B}=\angle \mathrm{E} \)，\( \angle \mathrm{F}=\angle \mathrm{C} \)且\( \mathrm{AB}=3 \mathrm{DE} \)。
要求
我們必須選擇正確的答案。
解答
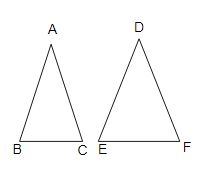
在三角形\( \mathrm{ABC} \)和\( \mathrm{DEF} \)中，\( \angle \mathrm{B}=\angle \mathrm{E} \)，\( \angle \mathrm{F}=\angle \mathrm{C} \)且\( \mathrm{AB}=3 \mathrm{DE} \)。
這意味著，
$\angle \mathrm{A}=\angle \mathrm{D}$
我們知道，
如果兩個三角形中對應兩個角相同，則根據 AAA 相似性準則，它們相似。
這裡，
$\triangle ABC$ 和 $\triangle DEF$ 不滿足任何全等規則（SAS、ASA、SSS）。
因此，三角形\( \mathrm{ABC} \)和\( \mathrm{DEF} \)相似但不全等。
更新於： 2022年10月10日
60 次檢視
廣告