天線理論 - 坡印廷向量

---

---

天線輻射電磁能量來傳輸或接收資訊。因此，這些電磁波與能量和功率相關，我們需要討論它們。電磁波既有電場又有磁場。

考慮任意時刻的波，它可以在兩個向量中觀察到。下圖顯示了電磁波中電場和磁場分量的表示。

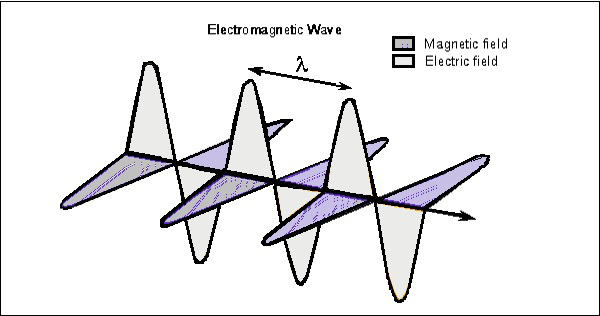
電波垂直於電磁波的傳播方向，而磁波則水平放置。這兩個場彼此成直角。

坡印廷向量

坡印廷向量描述了在任意給定時刻，電磁波每單位時間每單位面積的能量。約翰·亨利·坡印廷於1884年首次推匯出該向量，因此以他的名字命名。

定義 - “坡印廷向量給出每單位面積的能量傳遞速率”

或

“波每單位時間每單位面積攜帶的能量由坡印廷向量給出。”

坡印廷向量用Ŝ表示。

單位

坡印廷向量的SI單位為W/m²。

數學表示式

用於描述與電磁波相關的功率的量是瞬時坡印廷向量，其定義為

$$\hat{S} = \hat{E} \times \hat{H}$$

其中

• $\hat{S}$是瞬時坡印廷向量(W/m²)。

• $\hat{E}$是瞬時電場強度(V/m)。

• $\hat{H}$是瞬時磁場強度(A/m)。

這裡需要注意的重要一點是，在電磁波中，E 的幅值大於 H。但是，它們都貢獻了相同的能量。Ŝ 是一個向量，既有方向又有大小。Ŝ 的方向與波的速度相同。其大小取決於 E 和 H。

坡印廷向量的推導

為了更好地理解坡印廷向量，讓我們逐步瞭解坡印廷向量的推導過程。

讓我們想象一下，一個電磁波垂直於X軸（波沿X軸傳播）穿過一個面積（A）。在無窮小時間（dt）內穿過A時，波傳播距離（dx）。

$$dx = C\ dt$$

其中

$$C = 光速 = 3\times 10^{8}m/s$$ $$體積, dv = Adx = AC\ dt$$ $$d\mu = \mu\ dv = (\epsilon_{0}E^{2})(AC\ dt)$$ $$= \epsilon_{0} AC \ E^{2}\ dt$$

因此，在時間（dt）內每單位面積（A）傳遞的能量為 -

$$S = \frac{能量}{時間\times 面積} = \frac{dW}{dt\ A} = \frac{\epsilon_{0}ACE^{2}\ dt}{dt\ A} = \epsilon_{0}C\:E^{2}$$

由於

$$\frac{E}{H} = \sqrt{\frac{\mu_{0}}{\epsilon_{0}}} \ 則 S= \frac{CB^{2}}{\mu_{0}}$$

由於

$$C = \frac{E}{H} \ 則 S = \frac{EB}{\mu_{0}}$$ $$= \hat{S} = \frac{1}{\mu_{0}}(\hat{E}\hat{H})$$

Ŝ表示坡印廷向量。

上述方程給出了任意給定時刻每單位時間每單位面積的能量，稱為坡印廷向量。