電晶體組態

上一個
下一個

任何電晶體都有三個端子：發射極、基極和集電極。利用這三個端子，可以將電晶體以三種不同的可能組態連線到電路中，其中一個端子對輸入和輸出都共用。

三種組態型別為共基極、共發射極和共集電極組態。在每種組態中，發射極結都是正向偏置的，集電極結都是反向偏置的。

共基極（CB）組態

顧名思義，基極端子被用作電晶體輸入和輸出的共用端子。NPN和PNP電晶體的共基極連線如圖所示。

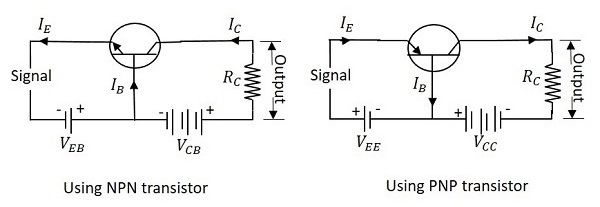
Common Base Connection

為了便於理解，讓我們考慮CB組態下的NPN電晶體。當施加發射極電壓時，由於它是正向偏置的，負極的電子會排斥發射極的電子，電流流過發射極和基極到集電極，從而形成集電極電流。在此過程中，集電極電壓VCB保持恆定。

在CB組態中，輸入電流是發射極電流IE，輸出電流是集電極電流IC。

電流放大係數（α）

當集電極電壓VCB保持恆定時，集電極電流（ΔIC）變化量與發射極電流（ΔIE）變化量的比率稱為電流放大係數。用α表示。

$\alpha = \frac{\Delta I_C}{\Delta I_E}$ 在恆定VCB下

集電極電流表達式

有了上述概念，讓我們嘗試為集電極電流推導一些表示式。

除了發射極電流之外，由於電子-空穴複合，還有一些基極電流IB流過基極端子。由於集電極-基極結是反向偏置的，因此由於少數載流子而產生另一電流。這可以理解為Ileakage（漏電流）。這是由於少數載流子引起的，因此非常小。

到達集電極端子的發射極電流為

$$\alpha I_E$$

總集電極電流

$$I_C = \alpha I_E + I_{leakage}$$

如果發射極-基極電壓VEB = 0，即使這樣，也仍然存在一個小的漏電流，可以稱為ICBO（輸出開路時的集電極-基極電流）。

因此，集電極電流可以表示為

$$I_C = \alpha I_E + I_{CBO}$$

$$I_E = I_C + I_B$$

$$I_C = \alpha (I_C + I_B) + I_{CBO}$$

$$I_C (1 - \alpha) = \alpha I_B + I_{CBO}$$

$$I_C = \frac{\alpha}{1 - \alpha}I_B + \frac{I_{CBO}}{1 - \alpha}$$

$$I_C = \left ( \frac{\alpha}{1 - \alpha} \right )I_B + \left ( \frac{1}{1 - \alpha} \right )I_{CBO}$$

因此，以上推導的是集電極電流的表示式。集電極電流的值取決於基極電流和漏電流以及所用電晶體的電流放大係數。

CB組態的特性

  • 這種組態提供電壓增益，但不提供電流增益。

  • 在VCB恆定的情況下，隨著發射極-基極電壓VEB的小幅增加，發射極電流IE會增加。

  • 發射極電流IE與集電極電壓VCB無關。

  • 集電極電壓VCB僅在低電壓下才能影響集電極電流IC，此時VEB保持恆定。

  • 輸入電阻Ri是在恆定集電極基極電壓VCB下，發射極-基極電壓（ΔVEB）變化量與發射極電流（ΔIE）變化量的比率。

$R_i = \frac{\Delta V_{EB}}{\Delta I_E}$ 在恆定VCB下

  • 由於輸入電阻值非常低，因此即使VEB值很小，也能產生很大的發射極電流IE。

  • 輸出電阻Ro是在恆定發射極電流IE下，集電極基極電壓（ΔVCB）變化量與集電極電流（ΔIC）變化量的比率。

$R_o = \frac{\Delta V_{CB}}{\Delta I_C}$ 在恆定IE下

  • 由於輸出電阻值非常高，因此VCB的大幅變化會導致集電極電流IC的變化非常小。

  • 這種組態對溫度升高具有良好的穩定性。

  • CB組態用於高頻應用。

共發射極（CE）組態

顧名思義，發射極端子被用作電晶體輸入和輸出的共用端子。NPN和PNP電晶體的共發射極連線如圖所示。

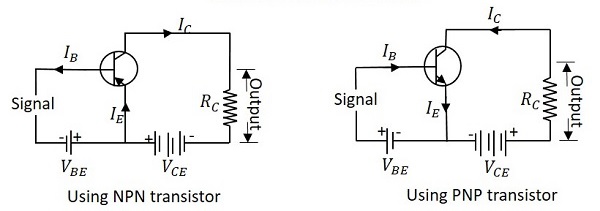
Common Emitter Connection

與CB組態一樣，發射極結是正向偏置的，集電極結是反向偏置的。電子的流動方式相同。這裡的輸入電流是基極電流IB，輸出電流是集電極電流IC。

基極電流放大係數（β）

集電極電流（ΔIC）變化量與基極電流（ΔIB）變化量的比率稱為基極電流放大係數。用β表示。

$$\beta = \frac{\Delta I_C}{\Delta I_B}$$

β和α之間的關係

讓我們嘗試推導基極電流放大係數和發射極電流放大係數之間的關係。

$$\beta = \frac{\Delta I_C}{\Delta I_B}$$

$$\alpha = \frac{\Delta I_C}{\Delta I_E}$$

$$I_E = I_B + I_C$$

$$\Delta I_E = \Delta I_B + \Delta I_C$$

$$\Delta I_B = \Delta I_E - \Delta I_C$$

我們可以寫成

$$\beta = \frac{\Delta I_C}{\Delta I_E - \Delta I_C}$$

除以ΔIE

$$\beta = \frac{\Delta I_C/\Delta I_E}{\frac{\Delta I_E}{\Delta I_E} - \frac{\Delta I_C}{\Delta I_E}}$$

我們有

$$\alpha = \Delta I_C / \Delta I_E$$

因此，

$$\beta = \frac{\alpha}{1 - \alpha}$$

從上式可以看出，當α接近1時，β趨於無窮大。

因此，共發射極連線中的電流增益非常高。這就是該電路連線在所有電晶體應用中廣泛使用的原因。

集電極電流表達式

在共發射極組態中，IB是輸入電流，IC是輸出電流。

我們知道

$$I_E = I_B + I_C$$

和

$$I_C = \alpha I_E + I_{CBO}$$

$$= \alpha(I_B + I_C) + I_{CBO}$$

$$I_C(1 - \alpha) = \alpha I_B + I_{CBO}$$

$$I_C = \frac{\alpha}{1 - \alpha}I_B + \frac{1}{1 - \alpha}I_{CBO}$$

如果基極電路開路，即如果IB = 0，

基極開路時的集電極發射極電流為ICEO

$$I_{CEO} = \frac{1}{1 - \alpha}I_{CBO}$$

將此值代入前一個方程，我們得到

$$I_C = \frac{\alpha}{1 - \alpha}I_B + I_{CEO}$$

$$I_C = \beta I_B + I_{CEO}$$

因此，獲得了集電極電流的方程。

膝電壓

在CE組態中，透過保持基極電流IB恆定，如果改變VCE，IC會增加到接近VCE的1v，然後保持恆定。VCE的這個值，在此值之前集電極電流IC隨VCE變化，稱為膝電壓。在CE組態下工作時，電晶體的工作電壓應高於此膝電壓。

CE組態的特性

  • 這種組態提供良好的電流增益和電壓增益。

  • 保持VCE恆定，當VBE小幅增加時，基極電流IB的增加速度比CB組態快。

  • 對於膝電壓以上的任何VCE值，IC近似等於βIB。

  • 輸入電阻Ri是在恆定集電極發射極電壓VCE下，基極發射極電壓（ΔVBE）變化量與基極電流（ΔIB）變化量的比率。

$R_i = \frac{\Delta V_{BE}}{\Delta I_B}$ 在恆定VCE下

  • 由於輸入電阻值非常低，因此即使VBE值很小，也能產生很大的基極電流IB。

  • 輸出電阻Ro是在恆定IB下，集電極發射極電壓（ΔVCE）變化量與集電極電流（ΔIC）變化量的比率。

$R_o = \frac{\Delta V_{CE}}{\Delta I_C}$ 在恆定IB下

  • CE電路的輸出電阻小於CB電路的輸出電阻。

  • 這種組態通常用於偏置穩定方法和音訊頻率應用。

共集電極（CC）組態

顧名思義，集電極端子被用作電晶體輸入和輸出的共用端子。NPN和PNP電晶體的共集電極連線如圖所示。

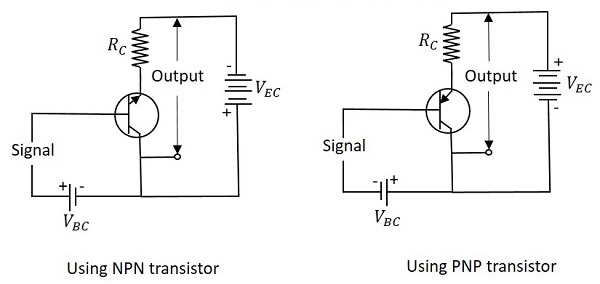
Common Collector Connection

與CB和CE組態一樣，發射極結是正向偏置的，集電極結是反向偏置的。電子的流動方式相同。這裡的輸入電流是基極電流IB，輸出電流是發射極電流IE。

電流放大係數（γ）

在共集電極（CC）組態中，發射極電流（ΔIE）變化量與基極電流（ΔIB）變化量的比率稱為電流放大係數。用γ表示。

$$\gamma = \frac{\Delta I_E}{\Delta I_B}$$

  • CC組態中的電流增益與CE組態相同。
  • CC組態中的電壓增益始終小於1。

γ和α之間的關係

讓我們嘗試在γ和α之間建立一些關係。

$$\gamma = \frac{\Delta I_E}{\Delta I_B}$$

$$\alpha = \frac{\Delta I_C}{\Delta I_E}$$

$$I_E = I_B + I_C$$

$$\Delta I_E = \Delta I_B + \Delta I_C$$

$$\Delta I_B = \Delta I_E - \Delta I_C$$

代入IB的值，我們得到

$$\gamma = \frac{\Delta I_E}{\Delta I_E - \Delta I_C}$$

除以ΔIE

$$\gamma = \frac{\Delta I_E / \Delta I_E}{\frac{\Delta I_E}{\Delta I_E} - \frac{\Delta I_C}{\Delta I_E}}$$

$$= \frac{1}{1 - \alpha}$$

$$\gamma = \frac{1}{1 - \alpha}$$

集電極電流的表示式

我們知道

$$I_C = \alpha I_E + I_{CBO}$$

$$I_E = I_B + I_C = I_B + (\alpha I_E + I_{CBO})$$

$$I_E(1 - \alpha) = I_B + I_{CBO}$$

$$I_E = \frac{I_B}{1 - \alpha} + \frac{I_{CBO}}{1 - \alpha}$$

$$I_C \cong I_E = (\beta + 1)I_B + (\beta + 1)I_{CBO}$$

以上是集電極電流的表示式。

共集電極配置的特性

  • 這種配置提供電流增益，但不提供電壓增益。

  • 在共集電極配置中，輸入阻抗高，輸出阻抗低。

  • 該電路提供的電壓增益小於1。

  • 集電極電流和基極電流之和等於發射極電流。

  • 輸入和輸出訊號同相。

  • 這種配置作為同相放大器輸出工作。

  • 該電路主要用於阻抗匹配。這意味著，從高阻抗源驅動低阻抗負載。

列印頁面
上一頁
下一頁
廣告