資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究無符號和有符號二進位制數
諸如整數之類的變數可以用兩種方式表示，即有符號和無符號。有符號數使用符號標誌或可以區分負值和正值。而無符號數僅儲存正數，而不儲存負數。
數字表示技術，例如：二進位制、八進位制、十進位制和十六進位制數字表示技術可以以有符號和無符號的方式表示數字。二進位制數系統是一種數字表示技術。它在數字系統中最流行和使用。二進位制系統用於表示二進位制量，這些量可以透過任何只有兩種工作狀態或可能條件的裝置來表示。例如，開關只有兩種狀態：開或關。
在二進位制系統中，只有兩個符號或可能的數字值，即 0 和 1。由任何只有 2 個工作狀態或可能條件的裝置表示。二進位制數透過新增 0b 字首或 2 字尾來指示。
二進位制數的表示
二進位制數可以以有符號和無符號的方式表示。無符號二進位制數沒有符號位，而有符號二進位制數使用符號位以及可以區分正數和負數。有符號二進位制數是有符號變數的一種特定資料型別。
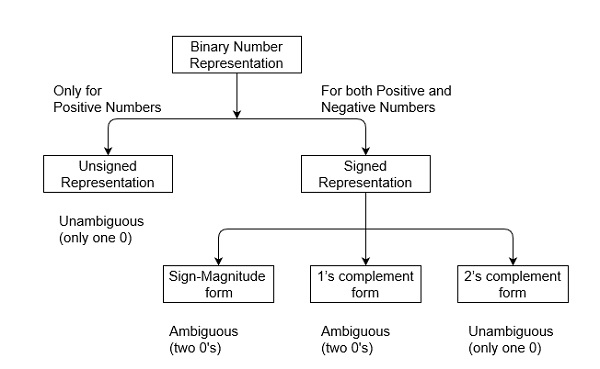
1. 無符號數
無符號數沒有任何符號，它們只能包含數字的幅值。因此，無符號二進位制數的表示僅為正數。例如，正十進位制數的表示預設情況下為正數。我們總是假設每個數字前面都有一個正號符號。
無符號二進位制數的表示
由於此無符號二進位制數中沒有符號位，因此 N 位二進位制數僅表示其幅值。零 (0) 也是無符號數。此表示形式只有一個零 (0)，它始終為正數。無符號數表示中的每個數字都只有一個唯一的二進位制等效形式，因此這是一種明確的表示技術。無符號二進位制數的範圍是從 0 到 (2n-1)。
示例-1：用無符號二進位制數表示十進位制數 92。
只需將其轉換為二進位制數，它僅包含給定數字的幅值。
= (92)10
= (1x26+0x25+1x24+1x23+1x22+0x21+0x20)10
= (1011100)2
這是十進位制數 92 的 7 位二進位制幅值。
示例-2：查詢 5 位無符號二進位制數的範圍。另外，查詢此範圍內的最小值和最大值。
由於無符號二進位制數的範圍是從 0 到 (2n-1)。因此，5 位無符號二進位制數的範圍是從 0 到 (25-1)，即從最小值 0（即 00000）到最大值 31（即 11111）。
2. 有符號數
有符號數包含符號標誌，此表示法區分正數和負數。此技術包含數字的符號位和幅值。例如，在負十進位制數的表示中，我們需要在給定的十進位制數前面加上負號。
有符號二進位制數的表示
有符號二進位制數有三種表示形式。由於存在額外的符號位，因此二進位制數零有兩種表示形式，要麼是正數 (0)，要麼是負數 (1)，因此表示不明確。但是，由於沒有數字零 (0) 的雙重表示，因此 2 的補碼錶示是明確的表示。它們是：符號幅值形式、1 的補碼形式和 2 的補碼形式，如下所述。
2.(a) 符號幅值形式
對於 n 位二進位制數，1 位保留用於符號符號。如果符號位的值為 0，則給定數字將為正數，否則如果符號位的值為 1，則給定數字將為負數。其餘 (n-1) 位表示數字的幅值。由於數字零 (0) 的幅值始終為 0，因此數字零 (0) 可以有兩種表示形式，正數 (+0) 和負數 (-0)，這取決於符號位的值。因此，由於數字零 (0) 的兩種表示形式，這些表示通常是不明確的。通常，符號位是表示的最重要位 (MSB)。符號幅值形式的範圍是從 (2(n-1)-1) 到 (2(n-1)-1)。
例如，6 位符號幅值形式二進位制數的範圍是從 (25-1) 到 (25-1)，即從最小值 -31（即 1 11111）到最大值 +31（即 0 11111）。零 (0) 有兩種表示形式，-0（即 1 00000）和 +0（即 0 00000）。
2.(b) 1 的補碼形式
由於數字的 1 的補碼是透過反轉給定數字的每一位獲得的。因此，我們以二進位制形式表示正數，以 1 的補碼形式表示負數。有一個額外的位用於符號表示。如果符號位的值為 0，則數字為正數，您可以直接以簡單的二進位制形式表示它，但如果符號位的值為 1，則數字為負數，您必須取給定二進位制數的 1 的補碼。您可以透過正數的 1 的補碼獲得負數，並透過使用負數的 1 的補碼獲得正數。因此，在此表示中，零 (0) 可以有兩種表示形式，這就是為什麼 1 的補碼形式也是不明確的形式。1 的補碼形式的範圍是從 (2(n-1)-1) 到 (2(n-1)-1)。
例如，6 位 1 的補碼形式二進位制數的範圍是從 (25-1) 到 (25-1)，即從最小值 -31（即 1 00000）到最大值 +31（即 0 11111）。零 (0) 有兩種表示形式，-0（即 1 11111）和 +0（即 0 00000）。
2.(c) 2 的補碼形式
由於數字的 2 的補碼是透過反轉給定數字的每一位並加上 1 到最低有效位 (LSB) 獲得的。因此，我們以二進位制形式表示正數，以 2 的補碼形式表示負數。有一個額外的位用於符號表示。如果符號位的值為 0，則數字為正數，您可以直接以簡單的二進位制形式表示它，但如果符號位的值為 1，則數字為負數，您必須取給定二進位制數的 2 的補碼。您可以透過正數的 2 的補碼獲得負數，並透過直接使用簡單的二進位制表示獲得正數。如果最高有效位 (MSB) 的值為 1，則取 2 的補碼，否則不取。因此，在此表示中，零 (0) 只有一個（唯一的）表示形式，它始終為正數。2 的補碼形式的範圍是從 (2(n-1)) 到 (2(n-1)-1)。
例如，6 位 2 的補碼形式二進位制數的範圍是從 (25) 到 (25-1)，即從最小值 -32（即 1 00000）到最大值 +31（即 0 11111）。零 (0) 有兩種表示形式，-0（即 1 11111）和 +0（即 0 00000）。
57K+ 瀏覽量
