二進位制數系統
二進位制數系統是一種數表示技術。它是數字系統中最流行和最常用的系統。二進位制系統用於表示二進位制量,這些量可以用任何只有兩種工作狀態或可能條件的裝置來表示。例如,開關只有兩種狀態:開或關。
在二進位制系統中,只有兩個符號或可能的數字值,即0和1。由任何只有2個工作狀態或可能條件的裝置表示。二進位制數通常透過新增0b字首或2字尾來表示。
每位數字都有一個權重,它是2的冪。二進位制系統中的每個位置都比前一個位置重要2倍,這意味著二進位制數的數值是透過將數字的每一位乘以該位出現的位置的值,然後將乘積相加來確定的。因此,它也是一種位置(或加權)數系統。
| 最高有效位 (MSB) | 二進位制小數點 | 最低有效位 (LSB) | |||
|---|---|---|---|---|---|
| 22 | 21 | 20 | 2-1 | 2-2 | 2-3 |
| 4 | 2 | 1 | 0.5 | 0.25 | 0.125 |
0V到0.8V之間的電壓範圍用於二進位制邏輯0,2V到5V之間的電壓範圍用於二進位制邏輯1。0.8V到2V之間的電壓範圍不用於,因為它可能會導致數位電路出錯。
示例1 - 數字125解釋為
125 = 1x26+1x25+1x24+1x23+1x22+0x21+1x20=1111101
這裡,最右邊的位1是最低有效位(LSB),最左邊的位1是最高有效位(MSB)。
示例2 - 數字90.75解釋為
90.75 = 1x26+0x25+1x24+1x23+0x22+1x21+0x20+1x2-1+1x2-2=1011010.11
這裡,最右邊的位1是最低有效位(LSB),最左邊的位1是最高有效位(MSB)。
示例3 - 將十進位制數21轉換為二進位制表示
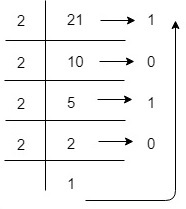
(21)10 =16+0+4+0+1 = 1x24+0x23+1x22+0x21+1x20 =(10101)2 So, decimal value 21 is equivalent to 10101 in Binary Number System.
二進位制數系統的應用
二進位制數系統在計算機技術中非常有用,計算機程式語言也使用二進位制數系統,這有助於數字編碼。二進位制數系統也可以用於布林代數。
優點和缺點
使用二進位制的主要優點是它是一個易於電子裝置表示的基數。二進位制數系統在編碼中也易於使用,計算更少,計算錯誤更少。
二進位制數的主要缺點是對於人類來說難以閱讀和編寫,因為等效十進位制數的二進位制數位數很多。
二進位制(2進位制)數的1的補碼和2的補碼
要獲得二進位制數的1的補碼,只需反轉給定的數字。例如,二進位制數110010的1的補碼是001101。
二進位制數的2的補碼是給定數字的1的補碼加上1到最低有效位(LSB)。例如,二進位制數10010的2的補碼是(01101) + 1 = 01110。


 資料結構
資料結構 網路
網路 關係資料庫管理系統(RDBMS)
關係資料庫管理系統(RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP