十六進位制數系統
十六進位制數系統是一種數的表示方法,其基數為16。這意味著只有16個符號或可能的數字值,它們是0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。其中A、B、C、D、E和F分別表示十進位制值10、11、12、13、14和15。表示任何一位數字只需要4位。十六進位制數通常用0x字首或h字尾表示。
每一位數字都有一個權重,它是16的冪。十六進位制系統中每個位置的有效數字都比前一位高16倍,這意味著十六進位制數的數值是透過將數字的每一位乘以該位出現的位數的值,然後將乘積相加來確定的。因此,它也是一個位置(或加權)數系統。
十六進位制數的表示
每個十六進位制數都可以用4位表示,每組位的值在0000(對於0)和1111(對於F = 15 = 8+4+2+1)之間。十六進位制數的等效二進位制數如下所示。
| 十六進位制數字 | 1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 |
| 二進位制 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| 十六進位制數字 | 8 | 9 | A = 10 | B = 11 | C = 12 | D = 13 | E = 14 | F = 15 |
| 二進位制 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
十六進位制數系統類似於八進位制數系統。十六進位制數系統提供了一種方便的方法,可以將大的二進位制數轉換為更緊湊的小組。
| 最高有效位 (MSB) | 十六進位制小數點 | 最低有效位 (LSB) | |||
|---|---|---|---|---|---|
| 162 | 161 | 160 | 16-1 | 16-2 | 16-3 |
| 256 | 16 | 1 | 1/16 | 1/256 | 1/4096 |
由於十六進位制數系統的基數為16,因此數字的最大值為15,不能超過15。在這個數系統中,十六進位制小數點左邊的連續位置的權重分別為160、161、162、163等等。類似地,十六進位制小數點右邊的連續位置的權重分別為16-1、16-2、16-3等等。這稱為16的冪次方。任何十六進位制數的十進位制值都可以透過將每個數字與其位置值相乘的乘積之和來確定。
示例-1 - 數字512解釋為
512=2x162+0x161+0x160=200
這裡,最右邊的位0是最低有效位(LSB),最左邊的位2是最高有效位(MSB)。
示例-2 - 數字2015.0625解釋為
2015.0625=7x162+13x161+15x160+1x16-1=7DF.10
這裡,最右邊的位0是最低有效位(LSB),最左邊的位7是最高有效位(MSB)。
示例-3 將十進位制數21轉換為十六進位制表示
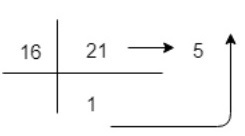
(21)10=1x161+5x160=(15)16 So, decimal value 21 is equivalent to 15 in Hexadecimal Number System.
十六進位制數系統的應用
十六進位制數系統通常用於計算機程式設計和微處理器。它還有助於描述網頁上的顏色。三種原色(即紅色、綠色和藍色)中的每一種都由兩位十六進位制數字表示,以建立255個可能的值,從而產生超過1600萬種可能的顏色。十六進位制數系統用於描述每個位元組的記憶體位置。對於計算機專業人員來說,這些十六進位制數也比二進位制數或十進位制數更容易閱讀和編寫。
優點和缺點
使用十六進位制數的主要優點是它使用更少的記憶體來儲存更多數字,例如,它用兩位數字儲存256個數字,而十進位制數用兩位數字儲存100個數字。此數系統也用於表示計算機記憶體地址。它只使用4位來表示二進位制中的任何數字,並且易於在十六進位制和二進位制之間進行轉換。以十六進位制形式處理輸入和輸出更容易。在資料科學、人工智慧和機器學習領域,它有很多優點。
十六進位制數系統的主要缺點是人們可能不容易閱讀和書寫,而且難以使用十六進位制數系統進行乘法、除法等運算。十六進位制數是處理計算機資料最困難的數系統。
十六進位制(16進位制)數的15的補碼和16的補碼
簡單來說,十六進位制數的15的補碼是從F(=15)中減去其每一位數字。例如,十六進位制數2030的15的補碼是FFFF - 2030 = DFCF。
十六進位制數的16的補碼是給定數字的15的補碼加上最低有效位(LSB)的1。例如,十六進位制數2020的16的補碼是(FFFF - 2030) + 1 = DFDF + 1 = DFE0。請注意,十六進位制數系統的最大數字是F(=15),因此F+1的加法將為0,進位為1。


 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP