八進位制數系統
八進位制數系統是一種數表示技術,其中基數為 8。這意味著只有 8 個符號或可能的數字值,分別是 0、1、2、3、4、5、6、7。它只需要 3 位來表示任何數字的值。八進位制數透過新增 0o 字首或 8 字尾來表示。
每個數字的位置都有一個權重,該權重是 8 的冪。八進位制系統中的每個位置都比前一個位置重要 8 倍,這意味著八進位制數的數值是透過將數字的每個數字乘以該數字出現的位置的值,然後將乘積相加來確定的。因此,它也是一種位置(或加權)數系統。
八進位制數的表示
每個八進位制數都可以使用僅 3 位來表示,每組位的值在 000(對於 0)和 111(對於 7 = 4+2+1)之間。八進位制數的等效二進位制數如下所示:
| 八進位制數字值 | 二進位制等效值 |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
八進位制數系統類似於十六進位制數系統。八進位制數系統提供了一種方便的方法,可以將大型二進位制數轉換為更緊湊和更小的組,但是這種八進位制數系統不太流行。
| 最高有效位 (MSB) | 八進位制點 | 最低有效位 (LSB) | |||
|---|---|---|---|---|---|
| 82 | 81 | 80 | 8-1 | 8-2 | 8-3 |
| 64 | 8 | 1 | 1/8 | 1/64 | 1/512 |
由於八進位制數系統的基值為 8,因此數字的最大值為 7,不能超過 7。在這個數系統中,八進位制點左側的連續位置的權重分別為 80、81、82、83 等。類似地,八進位制點右側的連續位置的權重分別為 8-1、8-2、8-3 等。這稱為 8 的基數冪。任何八進位制數的十進位制值都可以使用每個數字與其位置值的乘積之和來確定。
示例 1 - 數字 111 解釋為
111 = 1x82+5x81+7x80 = 157
這裡,最右邊的位 7 是最低有效位 (LSB),最左邊的位 1 是最高有效位 (MSB)。
示例 2 - 數字 65.125 解釋為
65.125 =1x82+0x81+1x80+1x8-1=101.10
這裡,最右邊的位 0 是最低有效位 (LSB),最左邊的位 1 是最高有效位 (MSB)。
示例 3 - 將十進位制數 21 表示為八進位制表示
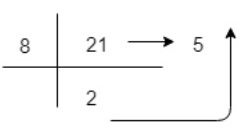
(21)10=2x81+5x80=(25)8 So, decimal value 21 is equivalent to 25 in Octal Number System.
八進位制數系統的應用
八進位制數不像以前那麼常見了。但是,當一個字中的位數是 3 的倍數時,會使用八進位制。它還用作表示 UNIX 系統上的檔案許可權以及 UTF8 數字等的簡寫。
優點和缺點
使用八進位制數的主要優點是它使用的數字比十進位制和十六進位制數系統少。因此,它具有更少的計算和更少的計算錯誤。它只需要 3 位來表示二進位制中的任何數字,並且易於在八進位制和二進位制之間轉換。以八進位制形式處理輸入和輸出更容易。
八進位制數系統的主要缺點是計算機不能直接理解八進位制數系統,因此我們需要八進位制到二進位制的轉換器。
八進位制(基數-8)數的 7 的補碼和 8 的補碼
簡單來說,八進位制數的 7 的補碼是從 7 中減去其每個數字。例如,八進位制數 127 的 7 的補碼是 777 - 127 = 650。
八進位制數的 8 的補碼是給定數字的 7 的補碼加上 1 到最低有效位 (LSB)。例如,八進位制數 320 的 8 的補碼是 (777 - 320) + 1 = 457 + 1 = 460。請注意,八進位制數系統的最大數字是 7,因此 7+1 的加法將為 0,進位為 1。


 資料結構
資料結構 網路
網路 關係型資料庫管理系統
關係型資料庫管理系統 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 程式設計
C 程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP