圓的切線

---

簡介

圓的切線是指與圓相切於一點的直線。所有與一個固定點等距的點的集合稱為圓，而平面上一組連續的點的集合稱為直線。在幾何學中，如果一條直線與圓在同一平面內，並且在圓周外與圓只有一個交點，即兩條線只有唯一的一個交點，那麼這條直線就被稱為圓的切線。從圓外一點可以畫出無數條這樣的直線。

圓的切線

與圓周上的恰好一個點相切於同一平面的直線稱為圓的切線。直線和圓的唯一公共點稱為切點。

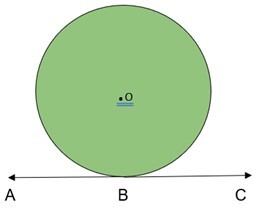
這是一個幾何表示，一個以 O 為圓心的圓在一個平面上的點 B 與直線 AC 相交。由於直線和圓的圓周只有一個公共點，因此 AC 成為圓的切線，B 為切點。這條直線位於圓的邊界之外。

方程為 x²+y²=a² 的圓在 (p,q) 點處的切線由 p²+q²=a² 給出。

圓的切線的性質

有各種性質定義了在特定點存在圓的切線。下面討論其中的一些性質：

性質	幾何表示
圓的切線在圓周上恰好與圓相切於一點。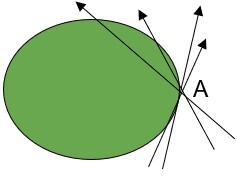
與圓的割線平行的切線只有兩條。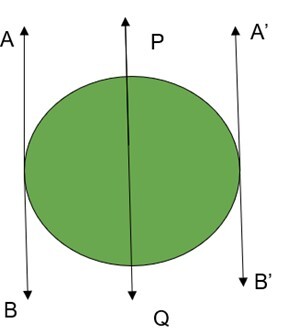
從圓外一點可以畫出兩條切線到圓。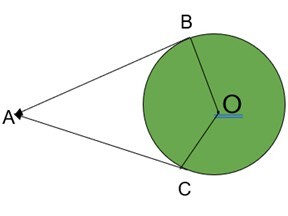

與圓的切線相關的定理

1. 圓上任意一點的切線總是與圓的半徑成 90° 角。

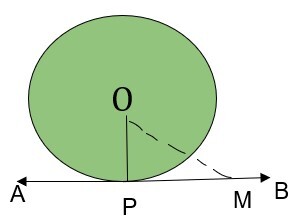
證明：在以 O 為圓心的圓的切線 AB 上取一點 M。因為切線和圓只有一個公共點，即 P，所以該點 M 位於圓外。因此，OM 比 OP（圓的半徑）長。

$$\mathrm{OM > OP}$$

這對於 AB 上除 P 之外的所有點都成立。

⇒ OP 是從點 O 到 AB 上任意點的最短距離。

由於垂直距離是點到線的最短距離，所以 OP 垂直於 AB。

2. 從圓外一點畫出的兩條切線的長度相等。

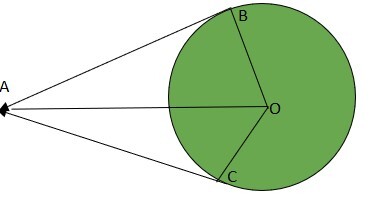
證明：AB=AC

證明：A 是位於以 O 為圓心的圓外的點。AB 和 AC 是從 A 到圓分別在 B 和 C 的兩條切線。

由於我們知道圓的切線垂直於半徑，

$$\mathrm{∴ ∠OBA=∠OCA}$$

⇒ OBA 和 OCA 是直角三角形。

現在，

在 OBA 和 OBC 中，

OB=OC（圓的半徑）

OA=OA（公共邊）

$$\mathrm{\angle OBA=\angle OCA=90°}$$

$$\mathrm{∴ △OBA≅△OCA}$$

$$\mathrm{⇒ AB=AC}$$

因此，從圓外一點畫出的兩條切線的長度相等。

例題

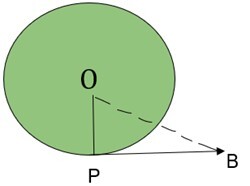
1. 如果圓的半徑為 3 釐米，OB = 5 釐米，求切線 PB 的長度（釐米）。

由於 OPB 是一個直角三角形，因為圓的切線在切點處垂直於半徑，

$$\mathrm{∴ (OP)^2+(PB)^2=(OB)^2}$$

$$\mathrm{\Rightarrow (3)^2+(PB)^2=(5)^2}$$

$$\mathrm{\Rightarrow (PB)^2=(5)^2-(3)^2}$$

$$\mathrm{\Rightarrow (PB)^2=16}$$

$$\mathrm{\Rightarrow PB=4cm}$$

2. 在給定圖形中，以 O 為圓心的圓在 A 和 B 處與∠ACB 的邊相切。如果∠BAC=80°，求∠BOC 的度數。

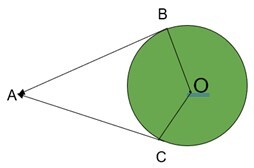
$$\mathrm{\angle BAC+\angle ACO+\angle COB+\angle OBA=360°}$$

這是因為四邊形的內角和等於 360°。

$$\mathrm{80°+90°+90°+ \angle BOC= 360°}$$

$$\mathrm{\angle BOC=100°}$$

3. 在給定圖形中，∠BOC=140°，求∠BAC。

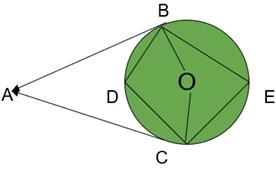
由於圓內角的大小是形成相同弧的圓心角大小的一半，

因此，

$$\mathrm{\angle BEC=1/2 \angle BOC}$$

$$\mathrm{\Rightarrow \angle BEC=70°}$$

現在，

$$\mathrm{\angle BAC+\angle ACO+\angle COB+\angle OBA=360°}$$

$$\mathrm{\Rightarrow \angle BAC=360°-90°-90°-70°}$$

$$\mathrm{\Rightarrow \angle BAC=110°}$$

結論

本教程將圓的切線描述為一條直線與圓在同一平面內相交的唯一公共點。一個圓可以有無限多條切線，但是從一個點只能畫出一條切線到圓。切線垂直於圓的半徑，即它與半徑成 90° 角。切線與圓相切的點稱為切點。圓的切線是一個有價值的資訊，因為它使我們能夠找出曲線在特定點處的曲線的斜率。方程為 x²+y²=a² 的圓在 (p,q) 點處的切線由 p²+q²=a² 給出。

常見問題

1. 兩個圓可以相互相切嗎？

切線是與圓相切於恰好一點的直線。因此，如果一個圓在同一平面上與另一個圓恰好相切於一點，那麼它們有一個共同點，因此，一個圓在該點與另一個圓相切。

2. 從圓周上一點和圓外一點可以畫出的切線的數量有什麼區別？

從圓周上一點只能畫出一條切線，因為切線與圓恰好相切於一點。但是，從圓外一點可以畫出兩條切線到圓，每條切線都與圓相切於一點。

3. 給出圓的切線的兩個現實生活中的例子。

• 腳踏車輪胎是一個在平面道路上行駛的圓，其中道路在輪胎上的每個點形成一個切線，因為腳踏車在移動。

• 球在蹺蹺板上滾動是另一個例子，其中蹺蹺板的表面在球滾下蹺蹺板時在球上的每個點都是切線。

4. 圓心與其切線之間的最小距離是多少？

圓心與其切線之間的最小距離是圓的半徑，因為切線上圓外的任何其他點都位於圓的邊界之外，這意味著它大於圓的半徑。

5. 切線可以是割線嗎？

圓的切線可以是割線的一種特殊情況，其中其相應弦的兩端點重合。