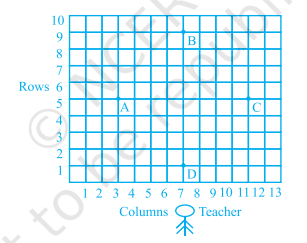
學校的學生們正在操場上按行列隊形進行操練。下圖顯示了四名學生 A、B、C 和 D 的位置。是否可以在操練中安排 Jaspal 的位置，使得他與這四名學生 A、B、C 和 D 的距離相等？如果可以，他的位置應該在哪裡？
"

已知條件

學校的學生們正在操場上按行列隊形進行操練。A、B、C 和 D 是四名學生的位置。

任務

我們必須找到是否可以安排 Jaspal 的位置，使得他與這四名學生 A、B、C 和 D 的距離相等。

解答

從圖中，我們可以觀察到四名學生 A、B、C 和 D 的位置分別是 (3,5)、(7,9)、(11,5) 和 (7,1)。

這四個頂點構成一個四邊形。

AB =√(7-3)²+(9-5)²

AB =√(4)²+(4)²

=√16+16

AB =4√2

BC =√(11-7)²+(5-9)²

=√(4)²+(-4)²

=√16+16

=4√2

CD =√(7-11)²+(1-5)²

=√(-4)²+(-4)²

=√16+16

=4√2

DA =√(3-7)²+(5-1)²

=√(-4)²+(4)²

=√16+16

=4√2

這裡，

AB=BC=CD=DA

因此，

Jaspal 的位置將是 AC 的中點 M(x, y)

根據截距公式，

中點 M(x, y) =( (x₁+x₃)/2, (y₁+y₃)/2 )

M(x, y) =( (3+11)/2, (5+5)/2 )

M(x, y) =(7,5)

因此，Jaspal 的位置（座標）是 (7,5)。

Tutorialspoint

更新於：2022年10月10日

瀏覽量：237

開啟你的職業生涯

完成課程獲得認證

開始學習