畫一個圓，並在圓上標記點\( \mathrm{A}, \mathrm{B} \)和\( \mathrm{C} \)，使得
(a) \( \mathrm{A} \)在圓上。
(b) \( \mathrm{B} \)在圓的內部。
(c) \( \mathrm{C} \)在圓的外部。
要做的
我們必須畫一個圓，並在其上標記點$A, B$和$C$，使得
(a) $A$在圓上
(b) $B$在圓的內部。
(c) $C$ 在圓的外部。
解答
使用圓規畫一個圓心為'$O$'的圓。
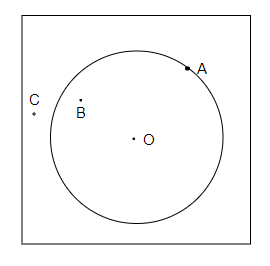
現在，
讓我們在圓上標記點'$A$'，在圓的內部標記點'$B$'，在圓的外部標記點'$C$'。
因此，
畫出了所需的圓，以及在所需位置的所需點$A, B$和$C$。
- 相關文章
- ABCD 是一個平行四邊形。透過\( \mathrm{A}, \mathrm{B} \)和\( \mathrm{C} \)的圓與\( \mathrm{CD} \)（如有必要則延長）相交於\( \mathrm{E} \)。證明\( \mathrm{AE}=\mathrm{AD} \)。
- 畫任意線段，例如\( \overline{\mathrm{AB}} \)。取任意一點\( \mathrm{C} \)位於\( \mathrm{A} \)和\( \mathrm{B} \)之間。測量\( AB, BC \)和\( AC \)的長度。是否\( AB=AC+CB \)？[注意：如果\( A, B, C \)是直線上的任意三點，使得\( AC+CB=AB \)，那麼我們可以確定\( \mathrm{C} \)位於\( \mathrm{A} \)和\( \mathrm{B} \)之間。]
- 如果\( \mathrm{B} \)是\( \overline{\mathrm{AC}} \)的中點，並且\( \mathrm{C} \)是\( \overline{\mathrm{BD}} \)的中點，其中\( \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D} \)位於一條直線上，請說明為什麼\( \mathrm{AB}=\mathrm{CD} \)？
- 在\( \Delta \mathrm{PQR} \)中，\( \mathrm{PD} \perp \mathrm{QR} \)，使得\( \mathrm{D} \)位於\( \mathrm{QR} \)上。如果\( \mathrm{PQ}=a, \mathrm{PR}=b, \mathrm{QD}=c \)和\( \mathrm{DR}=d \)，證明\( (a+b)(a-b)=(c+d)(c-d) \)。
- 畫一個圓心為\( \mathrm{C} \)，半徑為\( 3.4 \mathrm{~cm} \)的圓。畫任意弦\( \overline{\mathrm{AB}} \)。作\( \overline{\mathrm{AB}} \)的垂直平分線，並檢查它是否透過\( \mathrm{C} \)。
- 在圖中，一個圓內接於一個四邊形\( A B C D \)，其中\( \angle B=90^{\circ} \)。如果\( AD=23 \mathrm{~cm}, AB=29 \mathrm{~cm} \)和\( DS=5 \mathrm{~cm} \)，求圓的半徑\( r \)。”
- 在下圖中，A、B、C和D是圓上的四個點。\( \mathrm{AC} \)和\( \mathrm{BD} \)相交於一點\( \mathrm{E} \)，使得\( \angle \mathrm{BEC}=130^{\circ} \)和\( \angle \mathrm{ECD}=20^{\circ} \)。求\( \angle \mathrm{BAC} \)。”
- 在圖中，畫一個\( \triangle A B C \)外接一個半徑為\( 4 \mathrm{~cm} \)的圓，使得線段\( B D \)和\( D C \)的長度分別為\( 8 \mathrm{~cm} \)和\( 6 \mathrm{~cm} \)。求邊\( A B \)和\( A C \)的長度，當\( \triangle A B C \)的面積為\( 84 \mathrm{~cm}^{2} \)時。”
- \( A B \)是圓心為\( O \)，半徑為\( 4 \mathrm{~cm} \)的圓的一條弦。\( A B \)的長度為\( 4 \mathrm{~cm} \)。求弦\( A B \)形成的扇形的面積。
- 在圖中，一個圓與四邊形\( A B C D \)的四條邊都相切，其中\( AB=6 \mathrm{~cm}, BC=7 \mathrm{~cm} \)和\( CD=4 \mathrm{~cm} \)。求\( AD \)。”
- \( \mathrm{ABCD} \)是一個梯形，其中\( \mathrm{AB} \| \mathrm{DC} \)，並且\( \mathrm{P} \)和\( \mathrm{Q} \)分別是\( \mathrm{AD} \)和\( B C \)上的點，使得\( P Q \| D C \)。如果\( PD=18 \mathrm{~cm}, BQ=35 \mathrm{~cm} \)和\( \mathrm{QC}=15 \mathrm{~cm} \)，求\( \mathrm{AD} \)。
- 圓的直徑是連線圓上兩點並透過圓心的線段。在下圖中，\( \mathrm{AB} \)是圓的直徑；\( \mathrm{C} \)是圓心。用半徑\( (r) \)表示圓的直徑\( (d) \)。”
- 如果\( \mathrm{A}, \mathrm{B}, \mathrm{C} \)是直線上的三點，使得\( \mathrm{AB}=5 \mathrm{~cm}, \mathrm{BC}=3 \mathrm{~cm} \)和\( \mathrm{AC}=8 \mathrm{~cm} \)，那麼哪一點位於其他兩點之間？
- 點\( \mathrm{A}(2,9), \mathrm{B}(a, 5) \)和\( \mathrm{C}(5,5) \)是直角三角形\( \mathrm{ABC} \)的頂點，其中\( \mathrm{B} \)是直角頂點。求\( a \)的值，並求\( \triangle \mathrm{ABC} \)的面積。
- 一個圓的兩條弦\( \mathrm{AB} \)和\( \mathrm{CD} \)的長度分別為\( 5 \mathrm{~cm} \)和\( 11 \mathrm{~cm} \)，它們互相平行，並且位於圓心的兩側。如果\( \mathrm{AB} \)和\( C D \)之間的距離為\( 6 \mathrm{~cm} \)，求圓的半徑。
資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律學