資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究使用 Python 展示統計學中的離散均勻分佈
在統計學領域，機率分佈在對各種隨機現象進行建模和分析中發揮著重要作用。離散均勻分佈就是其中之一。當處理具有等可能結果的離散隨機變數時，它尤其有用。在本文中，我們將藉助 Python 程式設計，使用 scipy.stats.randint() 函式來探討離散均勻分佈。
Scipy 是一個功能強大的 Python 庫，用於科學分析和計算。stats 模組提供了用於統計分析的工具，包括機率分佈。
scipy.stats 模組中的 randint() 函式表示離散均勻變數，它從通用方法繼承其功能，作為 rv_discrete 類的例項。它允許有效地處理隨機離散變數。
randint() 函式的引數
randint 函式接受許多控制分佈行為的引數。這些引數包括：
low (loc) - 它是分佈的下界，表示可能的最小結果。它是包含的，即它可以是分佈的一部分。
high (loc+scale) - 它幾乎與 low 相反，是分佈的上界，表示可能的最大結果。但是它是排他的，即它不是分佈的一部分。
size (x) - 它是要生成的隨機變數的數量。因此，確定輸出的大小。
moments (mvsk) - 它由 'm' = 均值，'v' = 方差，'s' = 費舍爾偏度和 'k' = 費舍爾峰度組成。預設為 mv，它定義了要計算的統計矩。
建立離散均勻隨機變數
這與其他庫模組的實現類似，非常簡單。我們首先需要匯入 scipy 庫。讓我們建立一個隨機變數，它表示骰子的六個面。
示例
import scipy.stats as stats
uniformDiscreteVariable = stats.randint(low=1, high=7)
#created a unique discrete variable that resembles six outcomes of a dice
print("UDR: \n",uniformDiscreteVariable)
輸出
UDR: <scipy.stats._distn_infrastructure.rv_discrete_frozen object at 0x0000023787094040>
因此，我們建立了一個離散均勻整數變數，其下界為 1（包含）且上界為 7（不包含），因此可能結果的範圍為 1 到 6。
生成離散均勻值和機率分佈
我們已經定義了離散均勻變數，現在讓我們看看如何從同一個變數中生成隨機值或變數。讓我們也生成機率分佈。
rvs(low, high, loc=0, size=1, random_state=None) 方法幫助我們從定義的離散均勻變數中生成隨機變數。對於機率分佈，我們將使用 pmf(k, low, high, loc=0) 方法，它給出機率質量函式，即隨機事件每個結果的機率。下面我們嘗試列印生成的離散均勻變數和機率分佈。
示例
import scipy.stats as stats
uniformDiscreteVariable = stats.randint(low=1, high=7)
#created a unique discrete variable that resembles six outcomes of a dice
res = uniformDiscreteVariable.rvs(size=10)
#generating 10 random outputs i.e. dice rolls
probabDistrib = uniformDiscreteVariable.pmf(res)
print("UDR variates: ", res)
print("PD: ", probabDistrib)
輸出
UDR variates: [2 4 2 4 5] PD: [0.16666667 0.16666667 0.16666667 0.16666667 0.16666667]
上次，我們定義了一個離散均勻隨機變數，它公平地表示具有六個結果的骰子。在這裡使用 rvs 函式，我們從同一個變數生成了 10 個隨機輸出，即 10 次擲骰子結果的表示。機率函式顯示骰子中的每個數字都有相同的機率（1/6）。
圖形化視覺化
現在我們有了隨機變數和機率分佈，我們可以輕鬆地將它們繪製成圖形表示，以便更好地視覺化和理解。在 Python 中，matplotlib.pyplot 幫助我們對資料進行圖形化表示。
示例
import scipy.stats as stats
import matplotlib.pyplot as plt
uniformDiscreteVariable = stats.randint(low=1, high=7)
#created a unique discrete variable that resembles six outcomes of a dice
res = uniformDiscreteVariable.rvs(size=10)
#generating 10 random outputs i.e. dice rolls
probabDistrib = uniformDiscreteVariable.pmf(res)
print("UDR variates: ", res)
print("PD: ", probabDistrib)
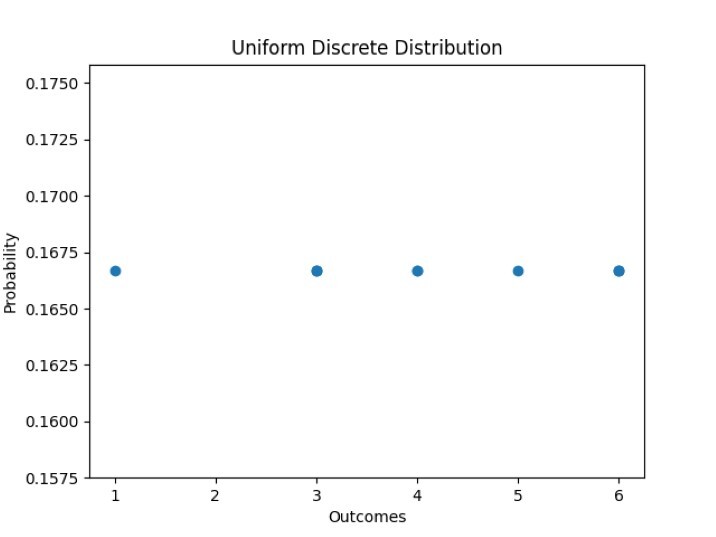
# Scatter plot for tossing a dice
plt.scatter(res, probabDistrib)
plt.xlabel('Outcomes')
plt.ylabel('Probability')
plt.title('Uniform Discrete Distribution')
plt.show()
輸出
UDR variates: [3 3 6 1 4 6 3 5 6 4] PD: [0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667]
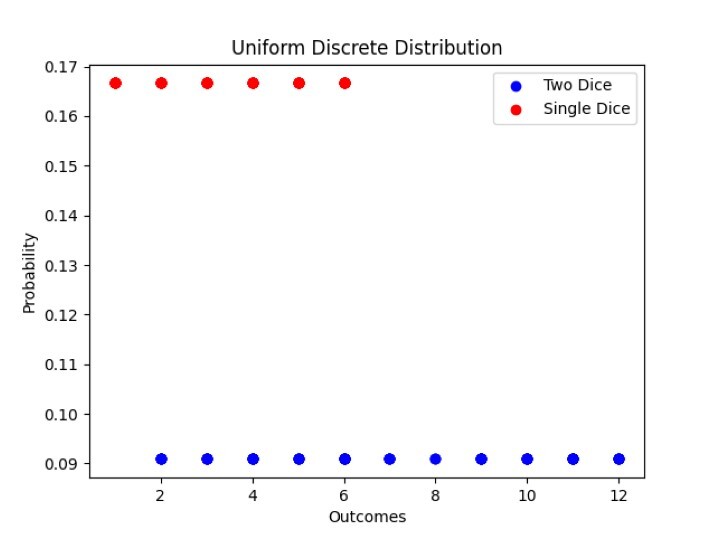
更改位置引數
我們可以輕鬆地調整 low 和 high 引數以及其他引數，以修改離散均勻分佈以適應各種場景。因此，讓我們嘗試生成兩個骰子隨機拋擲的離散均勻分佈以及單個骰子的分佈，並進行視覺化。
示例
import scipy.stats as stats
import matplotlib.pyplot as plt
uniformDiscreteVariable1 = stats.randint(low=2, high=13)
uniformDiscreteVariable2 = stats.randint(low=1, high=7)
# Generate random outcomes for two dice rolls
res1 = uniformDiscreteVariable1.rvs(size=100)
res2 = uniformDiscreteVariable2.rvs(size=100)
# Calculate probability distributions for the outcomes
probabDistrib1 = uniformDiscreteVariable1.pmf(res1)
probabDistrib2 = uniformDiscreteVariable2.pmf(res2)
print("UDR variates Two Dice: ", res1)
print("PD Two Dice: ", probabDistrib1)
print("UDR variates Single Dice: ", res2)
print("PD Single Dice: ", probabDistrib2)
# Scatter plot for tossing two dice
plt.scatter(res1, probabDistrib1, color='blue', label='Two Dice')
# Scatter plot for tossing a single dice
plt.scatter(res2, probabDistrib2, color='red', label='Single Dice')
plt.xlabel('Outcomes')
plt.ylabel('Probability')
plt.title('Uniform Discrete Distribution')
plt.legend()
plt.show()
輸出
UDR variates Two Dice: [ 5 3 5 10 2 11 2 12 4 9 4 9 6 10 8 5 11 9 2 8 9 3 12 6 5 11 2 7 3 12 3 11 6 4 5 6 6 7 11 12 3 12 9 9 7 11 12 10 9 10 2 6 11 6 10 10 11 10 12 6 6 4 5 6 4 10 9 7 8 10 6 11 9 9 3 7 4 11 3 12 6 2 6 11 4 11 2 9 2 9 6 3 4 11 4 4 7 6 5 6] PD Two Dice: [0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909 0.09090909] UDR variates Single Dice: [1 3 1 1 6 5 3 6 2 6 5 3 6 4 2 1 1 1 2 3 5 4 2 6 2 6 5 4 4 2 5 3 3 4 5 6 6 6 1 5 2 1 5 3 5 2 3 4 1 4 6 2 2 6 3 2 3 1 6 5 2 1 2 6 5 6 4 5 4 6 2 2 6 5 1 3 6 6 3 3 3 1 3 1 1 3 5 5 2 1 3 1 6 3 2 3 3 6 3 4] PD Single Dice: [0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667]
結論
本文即將結束，我們嘗試使用 Python 對離散均勻分佈（統計學中廣泛使用的一個基本概念）進行了視覺化。它定義了等可能結果的情況。Python 中 scipy.stats 模組和 randint() 方法形式的功能強大的工具幫助我們在統計學上建立對離散均勻資料的理解和實現。
透過理解其引數並使用正確的格式，我們可以輕鬆地建立、生成和視覺化離散均勻分佈。無論是模擬公平的擲骰子、生成隨機結果還是處理現實世界的資料，離散均勻分佈在統計學領域（包括機率論、金融和計算機科學）都是一個寶貴且通用的工具。
329 次瀏覽
