使用Python展示統計學中的冪對數正態分佈

---

在這篇文章中，我們將學習冪對數正態分佈、其應用和用途。我們將學習如何透過包括PDF和CDF在內的不同方法來分析該分佈。在此之前，讓我們看看什麼是冪正態分佈。

冪對數正態分佈

冪對數正態分佈是對數正態分佈的一種變體。唯一的區別是，我們透過對對數正態分佈應用冪變換來獲得冪對數正態分佈。冪正態分佈和冪對數正態分佈的區別在於，冪正態分佈是正態分佈的變體，而冪對數正態分佈是對數正態分佈的變體。兩者都具有可以定義分佈形狀的冪引數。

讓我們使用各種方法來檢視冪對數正態分佈：

方法一：隨機數生成

在此方法中，我們將從冪對數正態分佈生成隨機數。為了生成隨機數，我們使用scipy.stats模組。

示例

from scipy.stats import powerlognorm
import numpy as np
import matplotlib.pyplot as plt

c, s = 2.14, 0.446

x = 0.5
random_numbers = powerlognorm.rvs(c, s, size=1000)
plt.hist(random_numbers, bins=30, density=True, alpha=0.5)
plt.xlabel('Values')
plt.ylabel('Probability')
plt.title('Power Log-Normal Distribution')
plt.show()

輸出

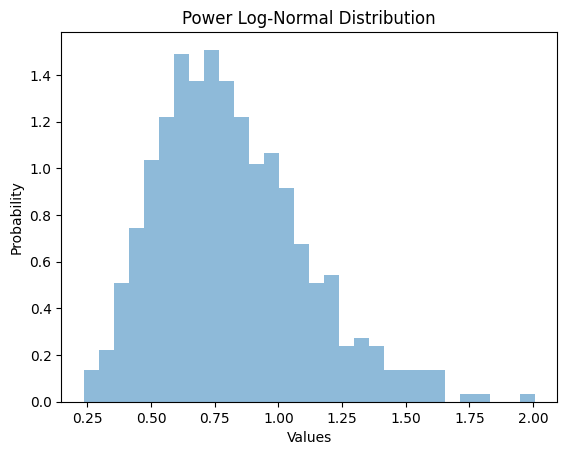
解釋

在此方法中，我們從scipy.stats匯入powerlognorm類。這裡，我們把c, s作為位置引數和形狀引數。使用powerlognorm.rvs()，我們從冪對數正態分佈生成了1000個隨機值，併為這些隨機值繪製了直方圖。

在函式中，我們從scipy.stats模組匯入了powerlognorm類，用於處理冪對數正態分佈。這裡c是位置引數，s是形狀引數。為了計算任何給定點的PDF，我們使用pdf()函式。

方法二：機率密度函式 (PDF)

冪對數正態分佈PDF觀察特定值的機率。它用於定義任何隨機變數的機率。為了分析任何特定點的PDF，我們將使用pdf()方法。

示例

from scipy.stats import powerlognorm
import numpy as np
import matplotlib.pyplot as plt
c, s = 2.14, 0.446

x = 1.5
pdf_ = powerlognorm.pdf(x, c, s)

print(pdf_)

輸出

0.12076527710927452

解釋

在此函式中，我們從scipy.stats模組匯入**powerlognorm**類。我們使用pdf()函式計算PDF，並將位置和形狀引數傳遞給pdf函式。

方法三：累積分佈函式 (CDF)

在此方法中，我們將使用累積分佈函式的PDF來描述小於或等於值x的隨機變數的值。我們可以使用cdf()函式計算CDF。

示例

from scipy.stats import powerlognorm
import numpy as np
import matplotlib.pyplot as plt
c, s = 2.14, 0.446

x = 1.5
cdf_ = powerlognorm.cdf(x, c, s)

print(cdf_)

輸出

0.9740141301157031

解釋

在此函式中，我們從scipy.stats模組匯入powernorm類，用於處理冪對數正態分佈。

方法三：視覺化冪對數正態分佈

讓我們視覺化冪對數正態分佈。

示例

from scipy.stats import powerlognorm
import numpy as np
import matplotlib.pyplot as plt

c, s = 2.14, 0.446

r = powerlognorm.rvs(c,s, size=1000)

plt.hist(r, bins=30, density=True, alpha=0.5)
plt.title('Power Log-Normal Distribution')
plt.xlabel('Values')
plt.ylabel('Probab')
plt.show()

輸出

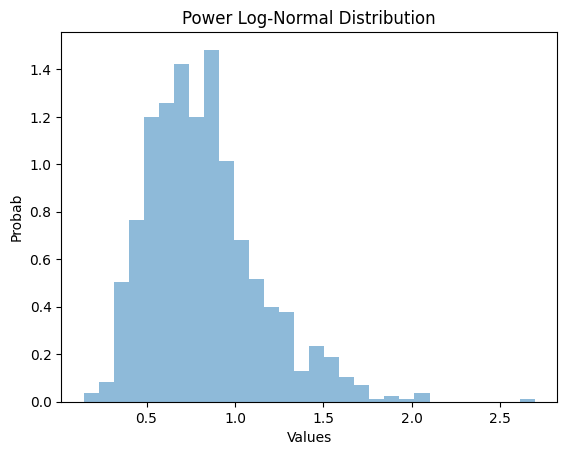
解釋

我們匯入了用於處理冪對數正態分佈和繪製圖形的庫。像往常一樣，我們使用powerlognorm.rvs()方法從冪對數正態分佈生成1000個隨機值。使用直方圖中的hist()函式繪製圖形。

因此，在這篇文章中，我們瞭解了冪對數正態分佈。我們看到了使用PDF的各種方法，包括生成隨機變數、計算PDF、CDF以及使用直方圖視覺化分佈。此外，我們還看到了如何將我們的資料擬合到（機率密度函式）PDF中。