使用 Python 展示統計學中的 Tukey-Lambda 分佈

---

介紹

統計學家巧妙地將機率分佈與相關資料來源結合起來，從而為資料庫中變數複雜性的廣泛而相關的假設提供（或否定）合理性。在這個領域，Tukey Lambda 分佈因其獨特的特徵而脫穎而出。憑藉其多功能性，Tukey 分佈可以有效地模擬各種形狀、尾部和不對稱程度不同的資料集。在我們深入探討 Python 實現之前，首先了解 Tukey-Lambda 分佈的基本特徵至關重要。

理解 Tukey-Lambda 分佈

在 20 世紀 60 年代，John W. Tukey 開發了 Tukey-Lambda 分佈——一種統計常數機率分佈。該分佈足夠靈活，可以適應多種形狀變化。與通常採用對稱和標準化尾部模式的傳統分佈相比，Tukey-Lambda 分佈允許可變性，因為它允許不對稱性和可適應的尾部趨勢，從而比其前身更全面地適應實際資料集的不規則性。

引數在定義分佈中起著核心作用

• Lambda (λ) − 提供非凡的形狀控制功能，此特徵定義了其他分佈在特定限制內分佈的區域。方便地從 -∞ 到 +∞ 的變化允許分佈中的奇異性與對稱性或無序性保持一致。

• 位置 (loc) − 移動此引數會影響資料沿 x 軸的橫向分散方式。

• 尺度 (scale) − 控制分佈的寬度，分佈的尺度因子就像一個主要的操縱者。

使用 Tukey-lambda 分佈意味著在沒有限制的情況下探索複雜的領域，這得益於其廣泛的適用性。

在 Python 中實現 Tukey-Lambda 分佈

由於 'numpy'、'matplotlib' 和 'scipy' 的存在，在 python 中操作 Tukey-Lambda 分佈簡化了流程。透過此過程，我們生成 Tukey-Lambda 分佈資料，然後使用程式設計工具以圖形方式描繪其機率密度函式 (PDF)。

示例

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import tukeylambda

# Parameters for the Tukey-Lambda distribution
lam = 0.5  # Lambda parameter
loc = 0    # Location parameter
scale = 2  # Scale parameter

# Generate random data from the Tukey-Lambda distribution
data = tukeylambda.rvs(lam, loc, scale, size=1000)

# Create a histogram of the generated data
plt.hist(data, bins=50, density=True, alpha=0.6, color='g', label='Histogram')

# Plot the PDF of the Tukey-Lambda distribution
x = np.linspace(tukeylambda.ppf(0.01, lam, loc, scale),
   tukeylambda.ppf(0.99, lam, loc, scale), 100)
plt.plot(x, tukeylambda.pdf(x, lam, loc, scale),
   'r-', lw=2, label='PDF')

plt.title('Tukey-Lambda Distribution')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.show()

輸出

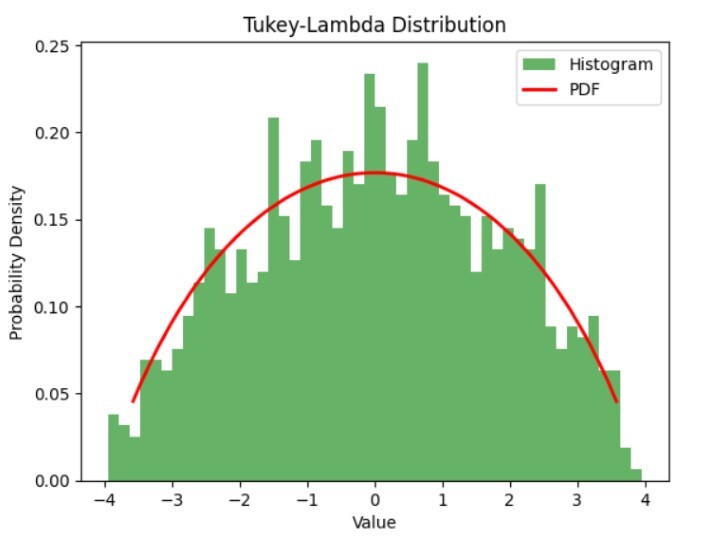
首先，讓我們匯入專案所需的內容。然後我們定義 Tukey-Lambda 分佈的引數：lambda、位置和尺度。使用 'tukeylambda.rvs()'，我們建立了一個包含 100 個數據點的樣本集，這些資料點符合預定的規範。

開始生成直方圖，我們的重點圍繞 'plt.hist()' 指令。經驗觀察轉化為這個描繪資料分佈的直方圖。執行 'tukey lambda.pdf()' 後，建立與現有圖形的疊加圖，以進一步闡明變數之間的潛在關係。

從 Tukey-Lambda 分佈生成隨機樣本

示例

import numpy as np
from scipy.stats import tukeylambda

# Define the parameters for the Tukey-Lambda distribution
lam = 1 # Lambda parameter
loc = 0    # Location parameter
scale = 3  # Scale parameter

# Create a Tukey-Lambda random variable
tukey_rv = tukeylambda(lam, loc, scale)

# Generate random samples from the Tukey-Lambda distribution
samples = tukey_rv.rvs(size=10)

# Print the generated samples
print("Generated samples:", samples)

輸出

Generated samples: [ 0.72782561 -2.85547765 -2.05191223 -1.49425406 -2.68583332 2.67587261 2.65954901 2.26647354 -2.17126878 2.43279198]

在此程式碼中，我們首先匯入所需的庫：numpy 和 scipy.stats.tukeylambda。後者專門用於處理 Tukey-Lambda 分佈。然後，我們定義 Tukey-Lambda 分佈的引數：Lambda (λ)、位置 (loc) 和尺度構成這些基本值。分佈的關鍵方面與列出的變數相關聯。

建立 Tukey-lambda 隨機變數需要使用適當選擇的引數呼叫 tukeylambda() 函式。使用 Tukey-Lambda 分佈的已定義引數，此隨機變數會隨機出現。透過使用預設的 Tukey lambda 方法，會從該分佈中隨機生成樣本。此處介紹的練習決定了 10 個例項的選擇。

分析具有不同引數的 Tukey-Lambda 分佈

示例

from scipy.stats import tukeylambda

def analyze_tukey_distributions(*parameters):
   for params in parameters:
      lam, loc, scale = params
      distribution = tukeylambda(lam, loc, scale)
       
      # Perform analysis on the distribution
      mean = distribution.mean()
      variance = distribution.var()
      
      print(f"For parameters {params}:")
      print(f"Mean: {mean}, Variance: {variance}")
      print()

# Various sets of parameters for Tukey-Lambda distribution
parameters_set1 = (0.5, 0, 2)
parameters_set2 = (-0.2, 1, 1.5)
parameters_set3 = (0.8, -1, 3)

analyze_tukey_distributions(parameters_set1, parameters_set2, parameters_set3)

輸出

For parameters (0.5, 0, 2):
Mean: 0.0, Variance: 3.4336293856408293

For parameters (-0.2, 1, 1.5):
Mean: 1.0, Variance: 16.841523810796254

For parameters (0.8, -1, 3):
Mean: -1.0, Variance: 4.253520146569082

解讀視覺化結果

透過直方圖繪製生成的資料的分佈，揭示了與 Tukey-Lambda 分佈的 PDF 的比較。藉助此疊加圖，我們可以評估生成的資料與預測分佈的符合程度。PDF 偏差表明生成的資料存在與分佈的定義特徵相矛盾的變化。

應用和意義

Tukey-Lambda 分佈的應用多種多樣，影響深遠。例如，在金融領域，股票回報經常表現出不穩定性，而 Tukey-Lambda 分佈可以更好地表示這些非常規模式。在資料看起來失真或尾部長度測量值異常的情況下，生物學可以更多地瞭解潛在的過程。

最佳實踐和注意事項

使用 varargs 和 Tukey-Lambda 分佈時，正確記錄引數順序及其意義至關重要。準確的文件將方便使用者理解，使他們能夠輕鬆提供正確的引數集。確保函式能夠正確處理各種引數組合排列。

結論

Tukey-Lambda 分佈是統計學中的一種多用途工具，它可以適應不符合規範的資料，使其有別於傳統的分佈。使用 Python，研究人員和分析師可以開發一個動態框架。結合分佈的 PDF 視覺化，可以深入瞭解其應用和適用性。Tukey-Lambda 分佈強調了統計方法在應對現實世界資料挑戰方面的靈活性和有效性。