使用 Python 在統計學中展示非中心 F 分佈

---

在給定的問題中，我們必須藉助 Python 及其庫來展示非中心 F 分佈。因此，我們將探討什麼是非中心 F 分佈以及如何使用 Python 來展示它。

瞭解非中心 F 分佈

非中心 F 分佈是統計學中的一種機率分佈，它主要用於分析給定資料中的方差。它透過使用非中心引數來使用中心 F 分佈，這些非中心引數用於進行偏差。

非中心 F 分佈用於確定觀察特定統計量的機率。此分佈的圖形是使用分子和分母的自由度生成的。它還使用非中心引數來顯示分佈。因此，分佈將根據這些引數的值發生變化。

該分佈如下所示：

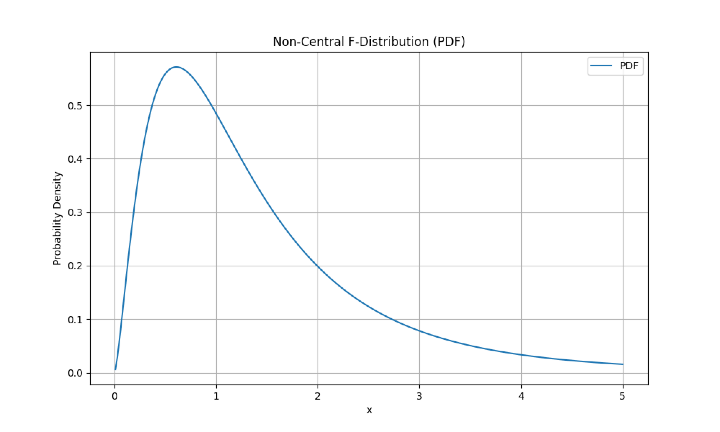
上述問題的邏輯

為了繪製此分佈，我們將使用 Python 庫“scipy.stats”，在程式中使用它之前，需要將其安裝在系統中。為了生成機率密度函式 (PDF) 和累積密度函式 (CDF)，我們將使用 stats.ncf() 函式。為了顯示分佈，我們必須生成遵循此分佈的隨機數。因此，我們將透過使用 scipy.stats 庫中的 noncentral_f() 函式來獲得它。此函式將接受自由度和非中心引數作為輸入。透過繪製 PDF 和 CDF，我們可以顯示非中心 F 分佈。

演算法

• 步驟 1 - 首先，我們必須匯入 Python 的必要庫來顯示非中心 F 分佈。在我們的程式中，我們將使用 Numpy、Matplotlib 和 Scipy.stats 庫。如果這些庫未安裝在系統上，則需要首先使用 pip install 'library_name' 進行安裝，然後我們才能在程式中使用這些庫。

import numpy as nmp
import scipy.stats as stats
import matplotlib.pyplot as mt_plt

• 步驟 2 - 匯入所需的庫後，我們將定義非中心 F 分佈的引數，例如分子自由度作為 num_df，分母自由度作為 deno_df，以及非中心引數作為 nc。

# Initialize the required parameters
num_df = 5  # numerator df
deno_df = 10  # denominator df
nc = 1  

• 步驟 3 - 現在，我們將生成用於繪製 F 分佈的 x 座標值。

# initialize the random numbers for x-values
x = nmp.linspace(0.1, 10, 1000)

• 步驟 4 - 接下來，我們將使用 stats.ncf() 函式計算機率密度函式的值並將其命名為 y_pdf，以及累積密度函式的值並將其命名為 y_cdf。

# compute PDF and CDF
y_pdf = stats.ncf.pdf(x, num_df, deno_df, nc)  
y_cdf = stats.ncf.cdf(x, num_df, deno_df, nc)  

• 步驟 5 - 計算所有所需的值後，我們將需要使用 matplotlib 繪製機率密度函式。在我們的繪圖中，我們將顯示 x 軸標籤、y 軸標籤和繪圖示題。

# plotting the Probability density function
mt_plt.figure(figsize=(8, 6))
mt_plt.plot(x, y_pdf, label='PDF')
mt_plt.xlabel('x')
mt_plt.ylabel('Probability Density')
mt_plt.title('Non-Central F-Distribution (PDF)')
mt_plt.legend()
mt_plt.grid(True)

• 步驟 6 - 現在，我們還將使用 matplotlib 庫繪製累積密度函式 (CDF)。

# plotting the cumulative density function
mt_plt.figure(figsize=(8, 6))
mt_plt.plot(x, y_cdf, label='CDF')
mt_plt.xlabel('x')
mt_plt.ylabel('Cumulative Probability')
mt_plt.title('Non-Central F-Distribution (CDF)')
mt_plt.legend()
mt_plt.grid(True)

• 步驟 7 - 在程式的最後，我們將使用 show() 函式顯示繪圖。

# Show the plots
mt_plt.show()

示例

import numpy as nmp
import scipy.stats as stats
import matplotlib.pyplot as mt_plt

# Initialize the required parameters
num_df = 5  # numerator df
deno_df = 10  # denominator df
nc = 1  

# initialize the random numbers for x-values
x = nmp.linspace(0.1, 10, 1000)

# compute PDF and CDF
y_pdf = stats.ncf.pdf(x, num_df, deno_df, nc)  
y_cdf = stats.ncf.cdf(x, num_df, deno_df, nc)  

# plotting the Probability density function
mt_plt.figure(figsize=(8, 6))
mt_plt.plot(x, y_pdf, label='PDF')
mt_plt.xlabel('x')
mt_plt.ylabel('Probability Density')
mt_plt.title('Non-Central F-Distribution (PDF)')
mt_plt.legend()
mt_plt.grid(True)

# plotting the cumulative density function
mt_plt.figure(figsize=(8, 6))
mt_plt.plot(x, y_cdf, label='CDF')
mt_plt.xlabel('x')
mt_plt.ylabel('Cumulative Probability')
mt_plt.title('Non-Central F-Distribution (CDF)')
mt_plt.legend()
mt_plt.grid(True)

# Show the plots
mt_plt.show()

輸出

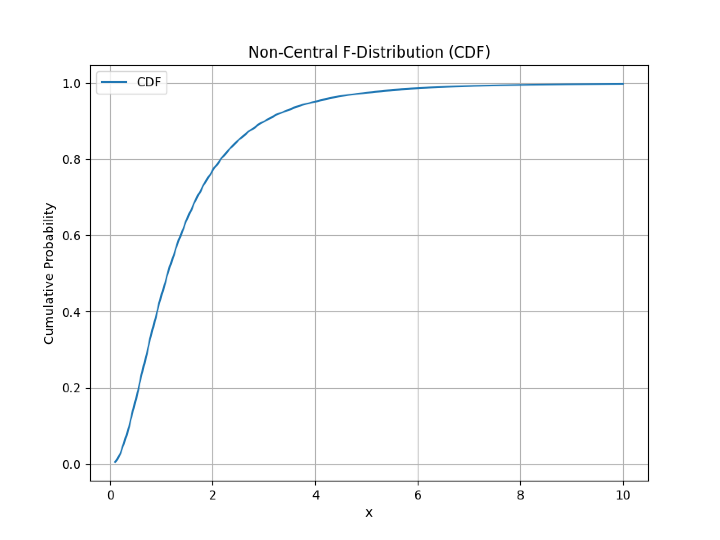
複雜度

生成隨機 x 值和繪製非中心 F 分佈的複雜度是線性的，為 O(n)，其中 n 是 x 軸上的點數。在我們的程式碼中，我們生成了 1000 個點來繪製 PDF 和 CDF。這兩個密度函式具有相同的複雜度。

結論

在本文中，我們藉助 Python 庫演示了非中心 F 分佈。正如我們使用分子自由度、分母自由度和非中心引數來生成 x 值一樣，這導致了線性的複雜度，這對於生成此分佈是有效的。