使用 Python 展示統計學中的帕累託分佈

---

帕累託分佈是一種冪律機率分佈，通常用於描述可測量的現象，例如社會、科學、地球物理或精算資料。它以義大利經濟學家、社會學家和土木工程師維爾弗雷多·帕累託的名字命名。帕累託分佈常用於模擬各種資料集的分佈，例如城市規模、網站流量和科學出版物的引用。

帕累托法則，也稱為 80/20 法則，表明在每種場景或系統中，20% 的投入會導致 80% 的產出。Python 提供了各種用於處理機率分佈的庫，例如 scipy.stats 庫。為了在 Python 中計算帕累託分佈，可以使用 scipy.stats 庫中的 pareto 函式，並將其形狀引數 alpha 和尺度引數 xm 作為引數。

語法

以下語法用於從帕累託分佈生成 500 個隨機數：

import numpy as np
   from scipy.stats import pareto
   data = pareto.rvs(alpha_value, 500, scale_value)
print(np.mean(data))

演算法

• 步驟 1 - 匯入庫。

• 步驟 2 - 定義形狀引數 (alpha) 和尺度引數 (xm)

• 步驟 3 - 給出生成隨機數的特定大小，並使用 'pareto.rvs' 函式。

• 步驟 4 - 列印生成的隨機數。

方法 1：這裡我們使用 scipy.stats 庫

示例 1

要從 alpha = 2 和 xm = 1 的帕累託分佈生成 500 個隨機數，我們可以使用以下程式碼：

import numpy as np
from scipy.stats import pareto
data = pareto.rvs(2, size=500, scale=1)
print(np.mean(data))

輸出

1.9138055526628364

此程式碼根據數字運算和質數定義的帕累託分佈生成 500 個隨機數。計算並列印生成的數字的平均值（均值）。這對於組織分佈統計資料並在 Python 中執行初步分析很有用。

示例 2

要從 alpha = 3 和 xm = 2 的帕累託分佈生成 700 個隨機數，我們可以使用以下程式碼：

import numpy as np
from scipy.stats import pareto
data = pareto.rvs(3, size=700, scale=2)
print(np.median(data))

輸出

2.517223926313278

此程式碼使用帕累託分佈生成 700 個隨機數，其中大小引數設定為 3，尺度引數設定為 2。計算並列印生成的數字的中位數（中間得分）。這可以用來檢查生成的數字的中間數字。

示例 3

要從 alpha = 5 和 xm = 1 的帕累託分佈生成 1000 個隨機數，我們可以使用以下程式碼：

import numpy as np
from scipy.stats import pareto
data = pareto.rvs(5, size=1000, scale=1)
print(np.median(data))

輸出

1.1557246772718455

在此程式碼中，從帕累託分佈生成 1000 個隨機數，大小引數設定為 3，尺度引數設定為 2。在此之後，計算並列印生成的數字的中位數。這給出了生成的數字的中位數。

方法 2：這裡我們使用 Numpy 庫

示例 1

要從 alpha = 2 和 xm = 1 的帕累託分佈生成 500 個隨機數，我們可以使用以下程式碼：

import numpy as np
alpha = 2
xm = 1
size = 500
data = np.random.pareto(alpha, size) + xm
print(np.mean(data))

輸出

1.8557392857152564

此程式碼根據數字運算和質數定義的帕累託分佈生成 500 個隨機數。它計算並列印生成的數字的平均值（均值）。

示例 2

要從 alpha = 4 和 xm = 2 的帕累託分佈生成 500 個隨機數，我們可以使用以下程式碼：

import numpy as np
alpha = 4
xm = 2
size = 500
data = np.random.pareto(alpha, size) + xm
print(np.mean(data))

輸出

2.33759634002971

此程式碼根據數字運算和質數定義的帕累託分佈生成 500 個隨機數。它計算並列印生成的數字的平均值（均值）。

示例 3

要從 alpha = 4 和 xm = 2 的帕累託分佈生成 700 個隨機數，我們可以使用以下程式碼：

import numpy as np
alpha = 4
xm = 2
size = 700
data = np.random.pareto(alpha, size) + xm
print(np.median(data))

輸出

2.202691921458917

在此程式碼中，帕累託分佈的 alpha 引數設定為 4，尺度 (xm) 設定為 2。在此之後，生成 700 個隨機數，這些隨機數根據帕累託分佈確定。計算並列印生成的數字的中位數。這給出了生成的數字的中位數。

注意 - 以上所有程式/程式碼每次都會給出不同的輸出，因為它們在程式中生成隨機數。

示例 4

在此程式/示例中，我們分別使用 pdf 和 cdf 方法計算帕累託分佈的機率密度函式 (PDF) 和累積分佈函式 (CDF)，並使用 matplotlib 繪製 PDF 和 CDF 以視覺化分佈。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import pareto
 
alpha = 2  # define shape parameter
xm = 1 	# define scale parameter
 
# Generate random numbers from a Pareto distribution
random_numbers = pareto.rvs(alpha, scale=xm, size=1000)
 
data = np.linspace(pareto.ppf(0.10, alpha, scale=xm), pareto.ppf(0.90, alpha, scale=xm), 100)
pdf = pareto.pdf(data, alpha, scale=xm) # Calculate the PDF
cdf = pareto.cdf(data, alpha, scale=xm) # Calculate the CDF
 
# Plotting the PDF and CDF
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(data, pdf, 'r', lw=2, label='PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Pareto Distribution PDF')
plt.legend()
 
plt.subplot(1, 2, 2)
plt.plot(data, cdf, 'b', lw=2, label='CDF')
plt.xlabel('x')
plt.ylabel('Cumulative Probability')
plt.title('Pareto Distribution CDF')
plt.legend() 
plt.show()

輸出

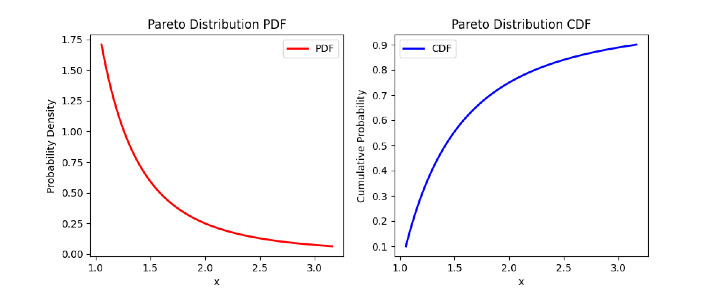
結論

總之，帕累託分佈是一種有效的統計工具，用於模擬具有少量極值和大量較小值的事件。帕累託分佈在各個領域都有廣泛的應用，因為它可以模擬收入差距、城市規模和其他經濟因素。透過使用 Python 模組（如 scipy.stats、Numpy 和 matplotlib），我們可以快速計算、擬合、視覺化和分析帕累託分佈，並獲得對這些情況的重要見解。