使用 Python 在統計學中展示冪函式分佈

---

在本文中，我們將學習統計學中的冪函式分佈。我們將檢查可以使用各種方法來分析冪函式分佈。在這篇文章中，我們還將瞭解如何在需要時擬合冪函式分佈。在此之前，讓我們先了解什麼是冪函式分佈。

冪函式分佈

這是一種用於對資料建模的連續機率分佈。使用冪函式，我們可以分析產生某些影響的小事件。使用冪函式，我們可以獲取有關罕見事件的詳細資訊，識別異常值，並可以對極值進行預測。

方法 1：使用 NumPy

在這種方法中，我們將使用 NumPy 庫中的 random.number.power 函式從冪函式分佈生成隨機數。我們還可以根據需要將形狀和大小引數傳遞給函式。

示例

import numpy as np

alpha = 2.0

random_numbers = np.random.power(alpha, size=50)
print(random_numbers)

輸出

[0.66577177 0.1679034  0.95589386 0.52785199 0.74796992 0.98980016
 0.56024262 0.93486863 0.74621463 0.34786775 0.68608517 0.75162506
 0.99800817 0.77750768 0.2619546  0.71702682 0.98451869 0.9473717
 0.6938956  0.62181687 0.87593638 0.97820392 0.61942659 0.3998725
 0.60715901 0.41922618 0.69290475 0.22384672 0.94772692 0.42051637
 0.37011727 0.46666447 0.80132086 0.51449008 0.70068973 0.48051619
 0.97054498 0.47957822 0.58914979 0.68553321 0.27976004 0.46894656
 0.82430862 0.66817431 0.54340906 0.61010354 0.61893109 0.0923075
 0.08385714 0.94302131]

解釋

在上面的函式中，我們定義了形狀引數，然後使用冪函式分佈生成 50 個隨機數。

random_numbers = np.random.power(alpha, size=50)

結果陣列將包含所有這些生成的數字。

方法 2：使用 SciPy

在這種方法中，我們將使用 SciPy 庫中的 scipy.Stats.Expon 模組。此模組提供了許多用於處理指數函式分佈的技術。我們可以使用 rvs 函式生成隨機數，並用於計算 pdf 和 cdf。

示例

from scipy.stats import expon

alpha = 2.0
random_numbers = expon.rvs(scale=alpha, size=100)

x = 0.5
pdf_value = expon.pdf(x, scale=alpha)

cdf_value = expon.cdf(x, scale=alpha)
print(cdf_value)

輸出

0.22119921692859515

解釋

在此程式中，我們從形狀引數為 2.0 的指數函式生成 50 個隨機數。在生成數字後，我們使用 rvs 函式計算了某個點 x 的 pdf 和 cdf。

方法 3：使用 Searborn

在此方法中，我們將使用 np.random.power，它將從冪函式分佈生成隨機數。使用 hist 函式，我們將顯示生成的隨機數的直方圖。

示例

import seaborn as sns

random_num = np.random.power(2.0, size=1000)

sns.distplot(random_num, hist=True, kde=True, bins=30)

輸出

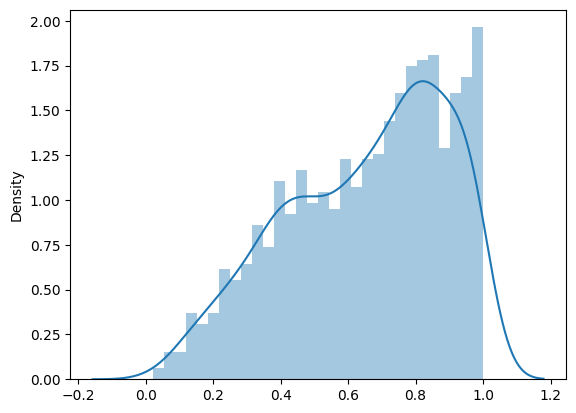
解釋

在此函式中，我們首先使用冪函式分佈生成隨機數。以下是生成隨機數的行。

random_num = np.random.power(2.0, size=1000)

生成隨機數後，我們將使用 matplotlib 庫中的 distplot 函式繪製直方圖以視覺化資料。

方法 4. 使用 Matplotlib

這是一個著名的 python 庫，用於繪製圖形並繪製資料的視覺表示。我們將使用 matplotlib 中的 plot 函式來視覺化冪函式分佈。

示例

import matplotlib.pyplot as plt

random_num = np.random.power(2.0, size=1000)

plt.hist(random_numbers, bins=30, density=True, alpha=0.5)
plt.xlabel('Values')
plt.ylabel('Probab')
plt.title('Power-fn Distribution')
plt.show()

輸出

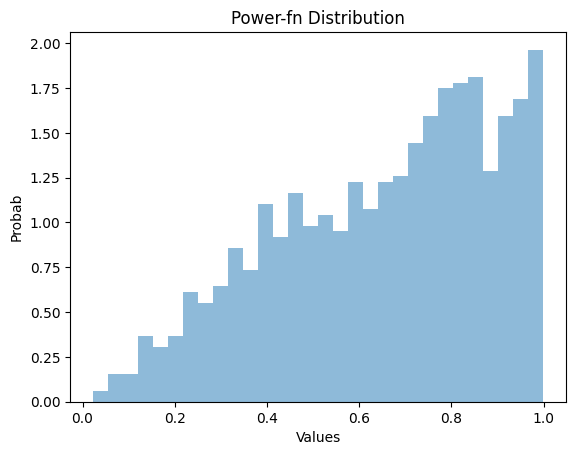
解釋

在此方法中，我們使用 np.random.power 從冪函式分佈生成隨機數。我們使用 matplotlib 庫中的 hist 函式來顯示生成的隨機數的直方圖。

方法 5. 將分佈擬合到資料

有時在使用 python 時，您會遇到想要擬合冪函式分佈的情況。因此，為了執行擬合，我們使用 scipy.stats.exponpow 模組中的 fit 方法，該方法可以根據資料估計形狀引數。

示例

from scipy.stats import exponpow
import numpy as np

data = np.array([0.5, 0.6, 0.7, 0.8, 0.9])

params = exponpow.fit(data)

random_num = exponpow.rvs(*params, size=50)
print(random_num)

輸出

[0.50115245 0.60597359 0.94355261 1.11336666 0.55644219 1.14871851
 0.83830517 0.84752829 0.52997894 0.79574141 0.59136949 0.67407663
 0.70188119 0.64854262 0.62878517 0.75472879 0.60225659 0.67842203
 0.96134614 0.72039852 0.56041962 0.50058046 0.84463519 0.74643548
 0.60791998 0.52271536 0.79289889 0.65340353 0.92378584 0.51754508
 0.51642979 0.71560587 0.69216641 0.59897395 0.80894948 0.50057274
 0.77434037 0.51578354 0.63737268 0.55335583 0.82872006 0.66339485
 0.50978196 0.68614946 0.73608196 0.58178696 0.85285616 1.03381135
 0.76055906 1.18414065]

因此，我們瞭解了展示冪函式分佈的各種方法。

我們學習瞭如何從冪函式生成隨機數，以及如何計算 PDF（機率密度函式）和 CDF（累積分佈函式）。使用 Seaborn 和 Matplotlib，我們繪製了任何統計資料的視覺表示。