SciPy - 空間

scipy.spatial 包利用Qhull 庫可以計算一組點的三角剖分、Voronoi 圖和凸包。此外，它還包含用於最近鄰點查詢的KDTree 實現以及用於各種度量距離計算的實用程式。

德勞內三角剖分

讓我們瞭解什麼是德勞內三角剖分以及如何在 SciPy 中使用它們。

什麼是德勞內三角剖分？

在數學和計算幾何中，對於平面中給定的一組離散點P，德勞內三角剖分DT(P)是這樣一種三角剖分，即P中沒有任何點位於DT(P)中任何三角形的圓內。

我們可以透過 SciPy 計算相同的結果。讓我們考慮以下示例。

from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()

上述程式將生成以下輸出。

共麵點

讓我們瞭解什麼是共麵點以及如何在 SciPy 中使用它們。

什麼是共麵點？

共麵點是位於同一平面上的三個或更多個點。回想一下，平面是一個平坦的表面，它向各個方向無限延伸。它通常在數學教科書中顯示為一個四邊形。

讓我們看看如何使用 SciPy 找到它。讓我們考慮以下示例。

from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanar

上述程式將生成以下輸出。

array([[4, 0, 3]], dtype = int32)

這意味著點 4 位於三角形 0 和頂點 3 附近，但未包含在三角剖分中。

凸包

讓我們瞭解什麼是凸包以及如何在 SciPy 中使用它們。

什麼是凸包？

在數學中，一組點 X 在歐幾里德平面或歐幾里德空間（或更一般地，在實數上的仿射空間）中的凸包或凸包絡是最小的凸集，它包含 X。

讓我們考慮以下示例來詳細瞭解它。

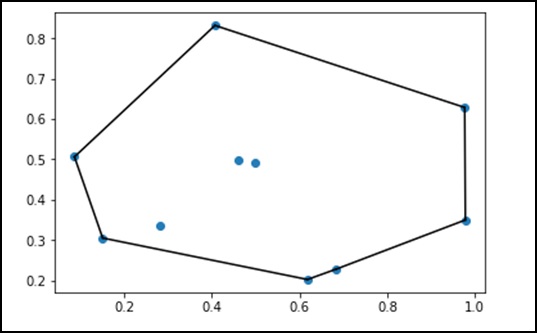
from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()

上述程式將生成以下輸出。