SciPy - CSGraph

CSGraph 代表壓縮稀疏圖，專注於基於稀疏矩陣表示的快速圖演算法。

圖表示

首先，讓我們瞭解什麼是稀疏圖以及它如何幫助圖表示。

什麼是稀疏圖？

圖只是一組節點，節點之間有連結。圖幾乎可以表示任何東西——社交網路連線，其中每個節點都是一個人，並連線到熟人；影像，其中每個節點都是一個畫素，並連線到相鄰畫素；高維分佈中的點，其中每個節點都連線到其最近鄰；以及你能想到的幾乎任何其他東西。

表示圖資料的一種非常有效的方法是使用稀疏矩陣：我們稱之為 G。矩陣 G 的大小為 N x N，而 G[i, j] 給出節點“i”和節點“j”之間連線的值。稀疏圖主要包含零——也就是說，大多數節點只有少量連線。事實證明，在大多數感興趣的情況下，此屬性都是正確的。

稀疏圖子模組的建立是由 scikit-learn 中使用的幾種演算法驅動的，這些演算法包括以下內容：

Isomap - 一種流形學習演算法，需要在圖中找到最短路徑。
層次聚類 - 一種基於最小生成樹的聚類演算法。
譜分解 - 一種基於稀疏圖拉普拉斯運算元的投影演算法。

作為一個具體的例子，假設我們想表示以下無向圖：

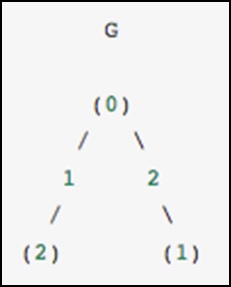
此圖有三個節點，其中節點 0 和 1 透過權重為 2 的邊連線，節點 0 和 2 透過權重為 1 的邊連線。我們可以構建密集、掩碼和稀疏表示，如以下示例所示，記住無向圖由對稱矩陣表示。

G_dense = np.array([ [0, 2, 1],
                     [2, 0, 0],
                     [1, 0, 0] ])
                     
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix

G_sparse = csr_matrix(G_dense)
print G_sparse.data

以上程式將生成以下輸出。

array([2, 1, 2, 1])

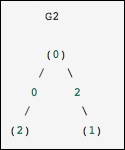
這與之前的圖相同，除了節點 0 和 2 透過權重為零的邊連線。在這種情況下，上面的密集表示會導致歧義——如果零是有意義的值，如何表示非邊。在這種情況下，必須使用掩碼或稀疏表示來消除歧義。

讓我們考慮以下示例。

from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
   [np.inf, 2, 0 ],
   [2, np.inf, np.inf],
   [0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.data

以上程式將生成以下輸出。

array([ 2., 0., 2., 0.])

使用稀疏圖的單詞階梯

單詞階梯是由劉易斯·卡羅爾發明的一種遊戲，其中單詞透過每次更改一個字母來連結。例如：

APE → APT → AIT → BIT → BIG → BAG → MAG → MAN

在這裡，我們已經用七步從“APE”到“MAN”，每次更改一個字母。問題是——我們能否使用相同的規則找到這些詞之間更短的路徑？這個問題自然地表示為一個稀疏圖問題。節點將對應於單個單詞，並且我們將建立連線那些最多相差一個字母的單詞對之間的邊。

獲取單詞列表

首先，當然，我們必須獲得有效單詞的列表。我正在執行 Mac，Mac 在以下程式碼塊中給出的位置有一個詞典。如果您使用的是不同的架構，則可能需要搜尋一下才能找到您的系統詞典。

wordlist = open('/usr/share/dict/words').read().split()
print len(wordlist)

以上程式將生成以下輸出。

現在我們想檢視長度為 3 的單詞，因此讓我們只選擇那些正確長度的單詞。我們還將消除以大寫字母開頭（專有名詞）或包含非字母數字字元（如撇號和連字元）的單詞。最後，我們將確保所有內容都小寫，以便稍後進行比較。

word_list = [word for word in word_list if len(word) == 3]
word_list = [word for word in word_list if word[0].islower()]
word_list = [word for word in word_list if word.isalpha()]
word_list = map(str.lower, word_list)
print len(word_list)

以上程式將生成以下輸出。

現在，我們有了一個包含 1135 個有效三個字母單詞的列表（確切數量可能會根據使用的特定列表而有所不同）。這些單詞中的每一個都將成為我們圖中的一個節點，我們將建立連線與每個單詞對相關聯的節點的邊，這些單詞對只相差一個字母。

import numpy as np
word_list = np.asarray(word_list)

word_list.dtype
word_list.sort()

word_bytes = np.ndarray((word_list.size, word_list.itemsize),
   dtype = 'int8',
   buffer = word_list.data)
print word_bytes.shape

以上程式將生成以下輸出。

(1135, 3)

我們將使用每個點之間的漢明距離來確定哪些單詞對是連線的。漢明距離衡量兩個向量之間不同條目的分數：任何兩個漢明距離等於 1/N1/N 的單詞，其中 NN 是單詞中字母的數量，這些字母在單詞階梯中是連線的。

from scipy.spatial.distance import pdist, squareform
from scipy.sparse import csr_matrix
hamming_dist = pdist(word_bytes, metric = 'hamming')
graph = csr_matrix(squareform(hamming_dist < 1.5 / word_list.itemsize))

在比較距離時，我們不使用相等性，因為這對於浮點值來說可能不穩定。只要單詞列表中沒有兩個條目相同，不等式就會產生所需的結果。現在，我們的圖設定好了，我們將使用最短路徑搜尋來查詢圖中任意兩個單詞之間的路徑。

i1 = word_list.searchsorted('ape')
i2 = word_list.searchsorted('man')
print word_list[i1],word_list[i2]

以上程式將生成以下輸出。

ape, man

我們需要檢查這些是否匹配，因為如果這些單詞不在列表中，輸出將出現錯誤。現在，我們只需要找到圖中這兩個索引之間的最短路徑即可。我們將使用迪傑斯特拉演算法，因為它允許我們僅為一個節點查詢路徑。

from scipy.sparse.csgraph import dijkstra
distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True)
print distances[i2]

以上程式將生成以下輸出。

5.0

因此，我們看到“ape”和“man”之間的最短路徑僅包含五個步驟。我們可以使用演算法返回的前驅來重建此路徑。

path = []
i = i2

while i != i1:
   path.append(word_list[i])
   i = predecessors[i]
   
path.append(word_list[i1])
print path[::-1]i2]

以上程式將生成以下輸出。

['ape', 'ope', 'opt', 'oat', 'mat', 'man']

列印頁面